(人教版)2023-2024学年九年级数学上册 23.3 课题学习 图案设计 同步分层训练(提升卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 五星红旗上的一个五角星图案如图所示,将图案绕五角星的中心至少旋转度能与自身重合,则为( )
 A、108 B、90 C、72 D、602. 观察下面图案在A、B、C、D四幅图案中,能通过原图案平移得到的是( )
A、108 B、90 C、72 D、602. 观察下面图案在A、B、C、D四幅图案中,能通过原图案平移得到的是( ) A、
A、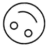 B、
B、 C、
C、 D、
D、 3. 能构成如图所示的图案的基本图形是( )
3. 能构成如图所示的图案的基本图形是( )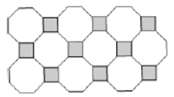 A、
A、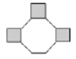 B、
B、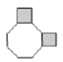 C、
C、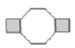 D、
D、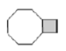 4. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
4. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( ) A、4种 B、5种 C、6种 D、7种5. 下列对下图的形成过程叙述正确的是( )
A、4种 B、5种 C、6种 D、7种5. 下列对下图的形成过程叙述正确的是( ) A、它可以看作是一只小狗绕图案的中心位置旋转 , , 形成的 B、它可以看作是相邻两只小狗绕图案的中心位置旋转形成的 C、它可以看作是相邻两只小狗绕图案的某条对称轴翻折而成的 D、它可以看作是左侧和上方的小狗分别向右侧和下方平移得到的6. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A、它可以看作是一只小狗绕图案的中心位置旋转 , , 形成的 B、它可以看作是相邻两只小狗绕图案的中心位置旋转形成的 C、它可以看作是相邻两只小狗绕图案的某条对称轴翻折而成的 D、它可以看作是左侧和上方的小狗分别向右侧和下方平移得到的6. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是( )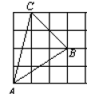 A、
A、 B、
B、 C、
C、 D、
D、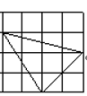 7. 由基本图案1得到图案2的方法是 ( )
7. 由基本图案1得到图案2的方法是 ( )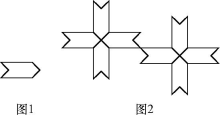 A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称8. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.
A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称8. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.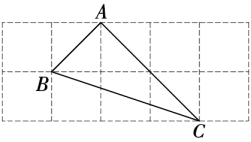 A、1 B、2 C、3 D、49. 如图为5×5的方格,点A,B,C均在格点上,点P在方格的其它格点上,且点A,B,C,P构成一个轴对称的点阵图,则符合条件的P点的位置有( )
A、1 B、2 C、3 D、49. 如图为5×5的方格,点A,B,C均在格点上,点P在方格的其它格点上,且点A,B,C,P构成一个轴对称的点阵图,则符合条件的P点的位置有( ) A、5个 B、4个 C、3个 D、2个10. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A、5个 B、4个 C、3个 D、2个10. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )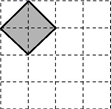 A、2种 B、3种 C、4种 D、5种
A、2种 B、3种 C、4种 D、5种二、填空题
-
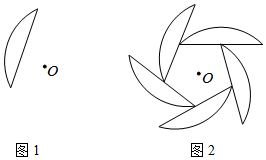
11. 利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α , 则α至少为 .
 12. 有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作次.
12. 有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作次.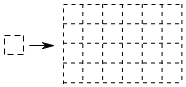 13. 如图: 为五个等圆的圆心,且 在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是.
13. 如图: 为五个等圆的圆心,且 在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是.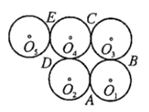 14. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.
14. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.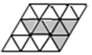 15. 如图,在平面直角坐标系xOy中,△ABC经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:.
15. 如图,在平面直角坐标系xOy中,△ABC经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:.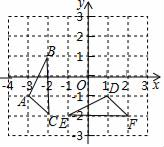
三、解答题
-
16. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有多少个?请分别在下图中涂出来,并画出这个轴对称图形的对称轴.

 17. 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在下面每个图形中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.
17. 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在下面每个图形中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.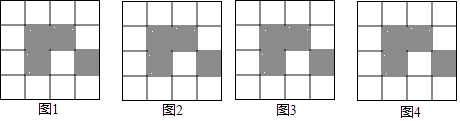 18. 如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?
18. 如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?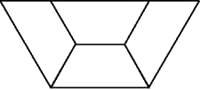 19. 如图,一栅栏顶部是由全等的三角形组成,下部分是由全等的矩形组成.请你运用平移、旋转、轴对称分析说明这个图形的形成过程.
19. 如图,一栅栏顶部是由全等的三角形组成,下部分是由全等的矩形组成.请你运用平移、旋转、轴对称分析说明这个图形的形成过程.
四、综合题
-
20. 观察如图①②③中阴影部分构成的图案
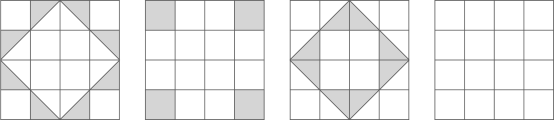
① ② ③ ④
(1)、请你写出这三个图案都具有的两个共同特征:(2)、请在图④中设计一个新的图案,使其满足(1)中的共同特征.21. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.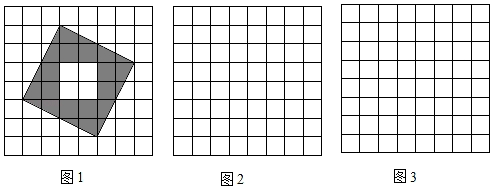 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.