(人教版)2023-2024学年九年级数学上册 23.3 课题学习 图案设计 同步分层训练(基础卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,经过旋转或轴对称得到 , 其中绕点逆时针旋转的是( )A、
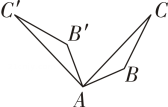 B、
B、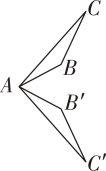 C、
C、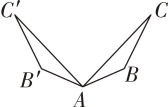 D、
D、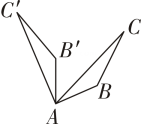 2. 下面是4个能完全重合的正六边形,请仔细观察、、、四个图案,其中与所给图形不相同的是( )
2. 下面是4个能完全重合的正六边形,请仔细观察、、、四个图案,其中与所给图形不相同的是( )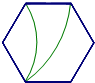 A、
A、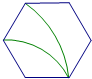 B、
B、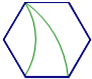 C、
C、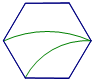 D、
D、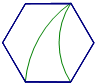 3. 下列大学校微可以看成是由图案自身的一部分经平移后得到的为( )A、
3. 下列大学校微可以看成是由图案自身的一部分经平移后得到的为( )A、 B、
B、 C、
C、 D、
D、 4. 2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移左图吉祥物“冰墩墩”可以得到的图形是( )
4. 2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移左图吉祥物“冰墩墩”可以得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 中国2010年上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.“海宝”的主体以汉字的“人”作为核心创意,既反应了中国文化的特色,又呼应了上海世博会会徽的设计理念.以下哪一个选项可由下图通过平移得到( )
5. 中国2010年上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”.“海宝”的主体以汉字的“人”作为核心创意,既反应了中国文化的特色,又呼应了上海世博会会徽的设计理念.以下哪一个选项可由下图通过平移得到( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列图案中,含有旋转变换的有( ) .
6. 下列图案中,含有旋转变换的有( ) . A、4个 B、3个 C、2个 D、1个7. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )A、
A、4个 B、3个 C、2个 D、1个7. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )A、 奥迪
B、
奥迪
B、 本田
C、
本田
C、 大众
D、
大众
D、 铃木
8. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( )
铃木
8. 如图,在 正方形网格中,已将图中的四个小正方形涂上阴影,若再从图中选一个涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么不符合条件的小正方形是( ) A、① B、② C、③ D、④9. 如图,图①,图②,图③,图④这四个图形中,可以由图A平移得到的是( )
A、① B、② C、③ D、④9. 如图,图①,图②,图③,图④这四个图形中,可以由图A平移得到的是( )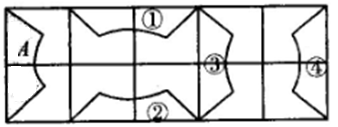 A、图① B、图② C、图③ D、图④10. 如图所示的各组图形中,表示平移关系的是( )A、
A、图① B、图② C、图③ D、图④10. 如图所示的各组图形中,表示平移关系的是( )A、 B、
B、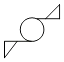 C、
C、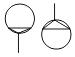 D、
D、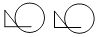
二、填空题
-
11. 正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有种.
 12. 如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有种
12. 如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有种 13. 如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=cm.
13. 如图所示的图案是由全等的图形拼成的,其中AD=0.5cm,BC=1cm,则AF=cm. 14. 如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 种.
14. 如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 种. 15. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
15. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
三、解答题
-
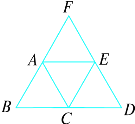
16. 下图中的四个小三角形都是等边三角形,边长为2 cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
 17. 如图,将其补全,使其成为中心对称图形.
17. 如图,将其补全,使其成为中心对称图形. 18. 如图,图(1)和图(2)是中心对称图形,仿照(1)和(2),完成(3)(4)(5)(6)的中心对称图形.
18. 如图,图(1)和图(2)是中心对称图形,仿照(1)和(2),完成(3)(4)(5)(6)的中心对称图形. 19. 某居民小区搞绿化,小区的居民们把一块矩形垃圾场地清理干净后,准备建几个花坛,老张说:花坛应该有圆有方;老李说:花坛和整个矩形空地应该成中心对称图案,这样比较漂亮.你能设计一个让大家都满意的方案吗?试试看(将你设计的方案画在下面的矩形方框中).
19. 某居民小区搞绿化,小区的居民们把一块矩形垃圾场地清理干净后,准备建几个花坛,老张说:花坛应该有圆有方;老李说:花坛和整个矩形空地应该成中心对称图案,这样比较漂亮.你能设计一个让大家都满意的方案吗?试试看(将你设计的方案画在下面的矩形方框中).
四、综合题
-
20. 观察如图①②③中阴影部分构成的图案
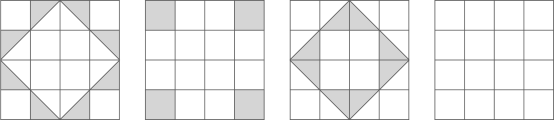
① ② ③ ④
(1)、请你写出这三个图案都具有的两个共同特征:(2)、请在图④中设计一个新的图案,使其满足(1)中的共同特征.21. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.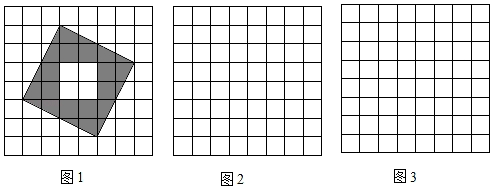 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
22. 如图都是由边长为1的小等边三角形构成的网格图,每个网格图中有3个小等边三角形已涂上阴影. (1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).23. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).23. 图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影: (1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
(1)、使得4个阴影小等边三角形组成一个轴对称图形.(2)、使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)