（人教版）2023-2024学年九年级数学上册 23.2中心对称同步分层训练（培优卷）

试卷更新日期：2023-11-07 类型：同步测试

进入出卷网下载

一、选择题

1. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，矩形 $A B C D$ 的对角线相交于点 $O$ ，过点 $O$ 的直线分别交 $A D$ 、 $B C$ 于点 $E$ 、 $F$ ，若两阴影三角形面积分别是 $3 c m^{2}$ ， $4 c m^{2}$ ，则矩形的面积是 $c m^{2}$ ．（）

A、 $14$ B、 $16$ C、 $24$ D、 $28$

查看试题解析
3. 若P(x，3)与点Q(4，y)关于原点对称，则xy的值是(　　)

A、12 B、-12 C、64 D、-64

查看试题解析
4. 将 $△ O B A$ 按如图方式放在平面直角坐标系中，其中 $∠ O B A = 90 °$ ， $∠ A = 30 °$ ，顶点 $A$ 的坐标为 $(1 ， \sqrt{3})$ ，将 $△ O B A$ 绕原点逆时针旋转，每次旋转60°，则第2023次旋转结束时，点 $A$ 对应点的坐标为（）

A、 $(- 1 ， \sqrt{3})$ B、 $(- \sqrt{3} ， 1)$ C、 $(- \frac{\sqrt{3}}{3} ， 1)$ D、 $(- 1 ， \frac{\sqrt{3}}{3})$

查看试题解析
5. 如图所示，矩形ABOC的顶点O（0，0），A（－2 $\sqrt{3}$ ， 2），对角线交点为P，若矩形绕点O逆时针旋转，每次旋转90°，则第74次旋转后点P的落点坐标为（）

A、(1， $\sqrt{3}$ ) B、（2，0） C、(1，- $\sqrt{3}$ ) D、( $\sqrt{3}$ ， -1)

查看试题解析
6. 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针45°后得到正方形 $O A_{1} B_{1} C_{1}$ ，依次方式，将正方形 $O A B C$ 绕点O连续旋转2021次得到正方形 $O A_{2021} B_{2021} C_{2021}$ ，如果点C的坐标为 $(0 ， 1)$ ，那么点 $B_{2021}$ 的坐标为（）

A、 $(- 1 ， 1)$ B、 $(- \sqrt{2} ， 0)$ C、 $(0 ， - \sqrt{2})$ D、 $(1 ， 0)$

查看试题解析
7. 如图，在平面直角坐标系中，以坐标原点O为顶点的正方形OBCD，其中点D（2，0），点B在y轴上，点C在第一象限，以BC为边在正方形OBCD外作等边△ABC，若将△ABC与正方形OBCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2020次旋转结束时，点A的坐标为（）

A、（1，2+ $\sqrt{3}$ ） B、（2+ $\sqrt{3}$ ， ﹣1） C、（﹣1，﹣2﹣ $\sqrt{3}$ ） D、（﹣2﹣ $\sqrt{3}$ ， ﹣1）

查看试题解析
8. 如图，在平面直角坐标系中， $△ A B C$ 的顶点 $A$ 在第一象限，点 $B 、 C$ 的坐标分别为 $(2 ， 1)$ 、 $(6 ， 1)$ ， $∠ B A C = 90^{\circ}$ ， $A B = A C$ ，直线 $A B$ 交 $y$ 轴于点 $P$ ，若 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 关于点 $P$ 成中心对称，则点 $A^{'}$ 的坐标为（）

A、（-4，-5） B、（-5，-4） C、（-3，-4） D、（-4，-3）

查看试题解析
9. 如图，将△ABC绕点C（0，﹣1）旋转180°得到△A'B'C，设点A的坐标为（a，b），则点A'的坐标为（）

A、（﹣a，﹣b） B、（﹣a，﹣b﹣1） C、（﹣a，﹣b+1） D、（﹣a，﹣b﹣2）

查看试题解析
10. 下列交通标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如图，点A是抛物线 $y = x^{2} - 4 x$ 对称轴上的一点，连接OA，以A为旋转中心将AO逆时针旋转90°得到AO′，当O′恰好落在抛物线上时，则三角形OAO′的面积为．

查看试题解析
12. 如图，在平面直角坐标中，对抛物线 $y = - 2 x^{2} + 2 x$ 在x轴上方的部分进行循环反复的轴对称或中心对称变换，若点A是该抛物线的顶点，则经过第2020次变换后所得的A点的坐标是．

查看试题解析
13. 如图，在直角坐标系中，四边形 $A B C D$ 是正方形，点A的坐标为 $(0 ， 1)$ ，点B的坐标为 $(2 ， 0)$ .若正方形 $A B C D$ 和正方形 $A_{1} B C_{1} B_{1}$ 关于点 $B$ 成中心对称：正方形 $A_{1} B C_{1} B_{1}$ 和正方形 $A_{2} B_{2} C_{2} B_{1}$ 关于点 $B_{1}$ 成中心对称；…，依此规律，则点 $C_{6}$ 的坐标为.

查看试题解析
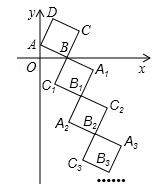14. 如图，在 $△ A O B$ 中， $∠ A O B = 90 °$ ， $O A = 3 ， O B = 4$ ．将 $△$ AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转，分别得到图②、图③、 $\dots$ ，则旋转得到的第13个三角形的直角顶点的坐标为．

查看试题解析
15. 如图，△ABC中，∠C＝90°，AC＝6，BC＝4，点O是AC的中点，以O为旋转中心，将△ABC绕点O旋转一周，A、B、C的对应点分别为A'、B'、C'，则BC'的最大值为．

查看试题解析

三、解答题

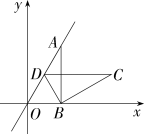
16. 如图，在平面直角坐标系xOy中，直线y= $\sqrt{3}$ x经过点A ，作AB⊥x轴于点B ，将△ABO绕点B顺时针旋转60°得到△CBD ，若点B的坐标为(2，0)，求点C的坐标.

查看试题解析
17. 如图，正方形网格中，每一个小正方形的边长都是1个单位长度，在平面直角坐标系内， $△$ ABC的三个顶点坐标分别为A(1，1)，B(3，2)，C(2，4)．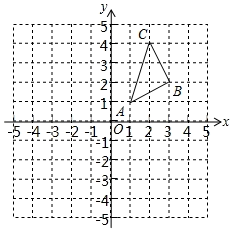

（ 1 ）画出 $△$ ABC关于原点O对称的 $△ A_{1} B_{1} C_{1}$ ，直接写出点 $A_{1}$ 的坐标；

（ 2 ）画出 $△$ ABC绕点O逆时针旋转90°后的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $A_{2} ， B_{2} ， C_{2}$ 的坐标．

查看试题解析
18.
如图，在平面直角坐标系中，点A的坐标是（1，1），如果将线段OA绕点O旋转135°，得线段OB，求点B的坐标？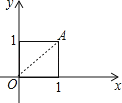

查看试题解析
19.
如图，点A坐标为（﹣2，3），将点A绕原点O顺时针旋转90°得点A′，求A′的坐标．

查看试题解析

四、综合题

20. 如图，在平面直角坐标系中，边长为4的正方形 $O A B C$ 的顶点A、C分别在y轴、x轴的正半轴上，点O在原点.现将正方形 $O A B C$ 绕点O按顺时针方向旋转，旋转角为 $θ$ ，当点A第一次落在直线 $y = x$ 上时停止旋转，旋转过程中， $A B$ 边交直线 $y = x$ 于点M， $B C$ 边交x轴于点N.

(1)、若 $θ = 30 °$ 时，求点A的坐标；

(2)、设 $△ M B N$ 的周长为P，在旋转正方形 $O A B C$ 的过程中，P值是否有变化？请证明你的结论；

查看试题解析
21. 如图，在平面直角坐标系中，抛物线y=ax²+bx+c的顶点坐标为P（2，9），与x轴交于点A，B，与y轴交于点C（0，5）．

(1)、求二次函数的解析式及点A，B的坐标；

(2)、设点Q在第一象限的抛物线上，若其关于原点的对称点Q′也在抛物线上，求点Q的坐标；

(3)、若点M在抛物线上，点N在抛物线的对称轴上，使得以A，C，M，N为顶点的四边形是平行四边形，且AC为其一边，求点M，N的坐标．

查看试题解析
22. 如图， $y_{1} = a x^{2} + b x$ 的图像交x轴于O点和A点，将此抛物线绕原点旋转180°得图像y₂ ， y₂与x轴交于O点和B点.

(1)、若 $y_{1} = 2 x^{2} - 3 x$ ，则y₂= .

(2)、设 $y_{1}$ 的顶点为C ，则当△ABC为直角三角形时，请你任写一个符合此条件的 $y_{1}$ 的表达式 .

查看试题解析
23. 如图，正方形ABCD 与正方形 $A_{1} B_{1} C_{1} D_{1}$ 关于某点中心对称.已知A， $D_{1}$ ，D三点的坐标分别是(0，4)，(0，3)，(0，2).

(1)、求对称中心的坐标：

(2)、写出顶点B，C， $B_{1} ， C_{1}$ 的坐标。

查看试题解析

（人教版）2023-2024学年九年级数学上册 23.2中心对称 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册 23.2中心对称同步分层训练（培优卷）