(人教版)2023-2024学年九年级数学上册 23.1图形的旋转 同步分层训练(培优卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
1. 如图,将边长为的正方形绕点逆时针旋转得到正方形 , 与交于点 , 那么图中点的坐标为( )
 A、 B、 C、 D、2. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )
A、 B、 C、 D、2. 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为BC边上一动点,连接AP,将线段AP绕点A顺时针旋转120°至AP′,则线段PP′的最小值为( )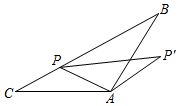 A、 B、 C、 D、3. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( )
A、 B、 C、 D、3. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( ) A、4 B、4 C、4 D、44. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )
A、4 B、4 C、4 D、44. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )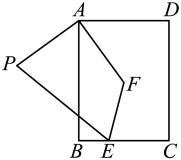 A、 B、 C、4 D、5. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( )
A、 B、 C、4 D、5. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( ) A、 B、 C、 D、6. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )
A、 B、 C、 D、6. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )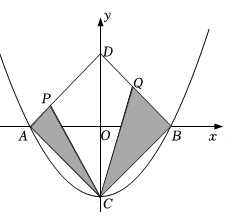 A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小7. 如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将APC绕着点A逆时针方向旋转60°得到AEF.则AE+PB+PC的最小值为( )
A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小7. 如图,已知∠BAC=60°,AB=4,AC=6,点P在△ABC内,将APC绕着点A逆时针方向旋转60°得到AEF.则AE+PB+PC的最小值为( )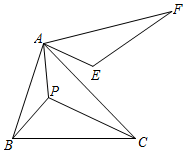 A、2 B、8 C、5 D、68. 在平面直角坐标系中,点A(-3,3),B(-4,1),C(-2,1),点M(2,m)绕坐标原点O逆时针旋转90°后,恰好落在△ABC内部(不包括边界),则m的取值范围为( )
A、2 B、8 C、5 D、68. 在平面直角坐标系中,点A(-3,3),B(-4,1),C(-2,1),点M(2,m)绕坐标原点O逆时针旋转90°后,恰好落在△ABC内部(不包括边界),则m的取值范围为( ) A、 <m< B、 <m< C、 <m< D、 <m<9. 已知正方形MNOK和正六边形ABCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是( )
A、 <m< B、 <m< C、 <m< D、 <m<9. 已知正方形MNOK和正六边形ABCDEF的边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转,……,在这样连续6次旋转的过程中,点B,M之间的距离可能是( ) A、1.4 B、1.1 C、0.8 D、0.510. 如图4,矩形ABCD绕点A逆时针旋转90*得矩形AEFG,连接CF,交AD于点P,M是CF的中点,连接AM,交EF于点Q。则下列结论:
A、1.4 B、1.1 C、0.8 D、0.510. 如图4,矩形ABCD绕点A逆时针旋转90*得矩形AEFG,连接CF,交AD于点P,M是CF的中点,连接AM,交EF于点Q。则下列结论:
①AM⊥CF;②△CDP≌△AEQ ;③连接PQ,则PQ= MQ;④若AB=2,BC=6,则MQ= 其中,正确结论的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在中, , , , , O为的中点,M为边上一动点,将绕点A逆时针旋转角得到 , 点M的对应点为 , 连接 , 在旋转过程中,线段的长度的最小值是 .
 12. 如图,在Rt中, , , , 是斜边的中线,将绕点A旋转,点B、C的对应点分别是点E、F,如果点F在射线上,那么= .
12. 如图,在Rt中, , , , 是斜边的中线,将绕点A旋转,点B、C的对应点分别是点E、F,如果点F在射线上,那么= .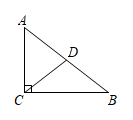 13. 如图,已知正方形ABCD的边长为6,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是 .
13. 如图,已知正方形ABCD的边长为6,点E是AB边上一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是 . 14. 如图,在正方形中,点是上一动点,点是的中点,绕点顺时针旋转得到 , 连接 , 给出结论:;;③若正方形的边长为2,则点在射线上运动时,有最小值其中结论正确的是 .
14. 如图,在正方形中,点是上一动点,点是的中点,绕点顺时针旋转得到 , 连接 , 给出结论:;;③若正方形的边长为2,则点在射线上运动时,有最小值其中结论正确的是 . 15. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .
15. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .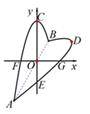
三、解答题
-
16. 如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,求FM的长.
 17. 如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
17. 如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF. (1)、求证:AE=DB;(2)、在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之和等于AB的长.18.
(1)、求证:AE=DB;(2)、在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之和等于AB的长.18.
发现:一次小组合作探究课上,嘉嘉将两个正方形按如图1所示的位置摆放(点E , A , D在同一条直线上),发现且 .
探究:将正方形绕点A按逆时针方向旋转(如图2),还能得到吗?若能,请给出证明;若不能,请说明理由.
19. 如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
 (1)、操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
(1)、操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,①△ADC是三角形;
②设△BDC的面积为 ,△AEC的面积为 ,则 与 的数量关系是 .
(2)、猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中 与 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.(3)、拓展探究:如图4,已知∠ABC=60°,点D是角平分线上一点,且BD=CD=4,DE∥AB交BC于点E.若在射线BA上存在点F,使S△DCF=S△BDE , 请直接写出相应的BF的长.四、综合题
-
20. 在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
 (1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.21. 如图①所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形 . 现将小长方形绕点C顺时针旋转至长方形 , 旋转角为 .
(1)、当点E恰好在AC上时,如图1,求∠ADE的大小;(2)、若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.21. 如图①所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形 . 现将小长方形绕点C顺时针旋转至长方形 , 旋转角为 .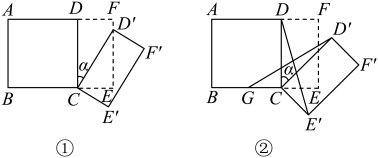 (1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.22. 如图,四边形是正方形,连接 , 将绕点A逆时针旋转α得到 , 连接 , O为的中点,连接.
(1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.22. 如图,四边形是正方形,连接 , 将绕点A逆时针旋转α得到 , 连接 , O为的中点,连接. (1)、如图1,当时,求证:.(2)、如图2,当时,(1)中的结论还成立吗?请说明理由.23. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D.
(1)、如图1,当时,求证:.(2)、如图2,当时,(1)中的结论还成立吗?请说明理由.23. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D. (1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.
(1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.