(人教版)2023-2024学年九年级数学上册 23.1图形的旋转 同步分层训练(提升卷)
试卷更新日期:2023-11-07 类型:同步测试
一、选择题
-
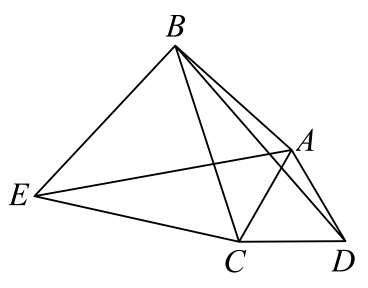
1. 如图,将绕着点按顺时针方向旋转 , 点落在位置,点落在位置,若 , 则的度数是( )
 A、
A、
B、
C、
D、2. 如图,将△ABC绕点A旋转到△AB1C1 , 有下列说法:
①AC=AB;②BC=B1C1;③∠BAC=∠B1AC1;④∠CAC1=∠BAB1 .
其中正确的有( ).
A、1个 B、2个 C、3个 D、4个3. 如图,将一个直角三角尺直立在桌面上向右翻滚.下列四个说法中,正确的个数是( ).①图①→图②是旋转;②图①→图③是平移;
③图①→图④是平移; ④图②→图③是旋转.
 A、1个 B、2个 C、3个 D、4个4. 将如图所示的图案绕其中心旋转n°时与原图案重合,则n的最小值是( ).
A、1个 B、2个 C、3个 D、4个4. 将如图所示的图案绕其中心旋转n°时与原图案重合,则n的最小值是( ).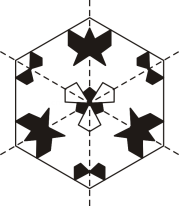 A、60 B、90 C、120 D、1805. 如图,已知中,于点 , 以点为中心,取旋转角等于 , 把顺时针旋转,得到 , 连接若 , , 则的大小为( )
A、60 B、90 C、120 D、1805. 如图,已知中,于点 , 以点为中心,取旋转角等于 , 把顺时针旋转,得到 , 连接若 , , 则的大小为( )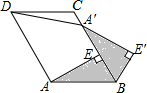 A、 B、 C、 D、6. 如图所示,Rt的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将Rt绕原点按顺时针方向旋转后得到 , 则点的对应点的坐标为( ).
A、 B、 C、 D、6. 如图所示,Rt的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将Rt绕原点按顺时针方向旋转后得到 , 则点的对应点的坐标为( ). A、 B、 C、 D、7. 下列说法中,正确的有( ).
A、 B、 C、 D、7. 下列说法中,正确的有( ).①图形旋转时,图形上的每一个点都绕旋转中心旋转了相同的角度;
②图形旋转时,对应点与旋转中心的距离相等;
③图形旋转时,对应线段相等,对应角相等,图形的形状和大小不变;
④两个图形成中心对称,可看作是一个图形绕着对称中心旋转180°得到另一个图形.A、1个 B、2个 C、3个 D、4个8. 如图所示,将绕点按顺时针方向旋转,使点落在AB边上点处,此时,点的对应点恰好落在BC边的延长线上.下列结论中,错误的是( ). A、 B、 C、 D、平分9. 下列现象不属于旋转的是( ).A、传送带传送货物 B、飞速转动的电扇 C、钟抎的抎动 D、自行车车轮的运动10. 如图所示,把是直角的绕点按顺时针方向旋转 , 把点转到点得 , 则下列结论中,错误的是( ).
A、 B、 C、 D、平分9. 下列现象不属于旋转的是( ).A、传送带传送货物 B、飞速转动的电扇 C、钟抎的抎动 D、自行车车轮的运动10. 如图所示,把是直角的绕点按顺时针方向旋转 , 把点转到点得 , 则下列结论中,错误的是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为25,DE=2,则AE的长为 .
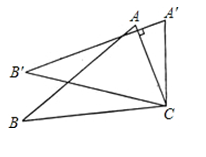
 12. 如图,将腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°得到△AB'C',则图中阴影部分的面积为
12. 如图,将腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°得到△AB'C',则图中阴影部分的面积为 13. 如图,将左边的长方形绕点B按顺时针方向旋转一定角度后,位置如右边的长方形,则∠CBA的度数是
13. 如图,将左边的长方形绕点B按顺时针方向旋转一定角度后,位置如右边的长方形,则∠CBA的度数是 14. 如图,将△AOB绕点O逆时针方向旋转45°后得到△COD.若∠AOB=15° ,则∠AOD的度数是
14. 如图,将△AOB绕点O逆时针方向旋转45°后得到△COD.若∠AOB=15° ,则∠AOD的度数是 15. 如图,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45.将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为
15. 如图,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45.将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为
三、解答题
-
16. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
 17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数.
17. 如图,在中, , 将绕点A顺时针方向旋转到的位置,连接 , 求的度数. 18. 如图,将矩形绕点C顺时针旋转得到矩形 , 点B与点E对应,点E恰好落在边上,交于点H,求证:.
18. 如图,将矩形绕点C顺时针旋转得到矩形 , 点B与点E对应,点E恰好落在边上,交于点H,求证:. 19. 如图,在中, , 将绕点C逆时针旋转50°得到 , 且于点D,求的度数.
19. 如图,在中, , 将绕点C逆时针旋转50°得到 , 且于点D,求的度数.
四、综合题
-
20. 如图,在中, , 将绕点A旋转一定的角度得到 , 且点E恰好落在边BC上.
 (1)、求证:AE平分;(2)、连接BD,求证: .21. 如图1,点E为正方形内一点, , 将绕点B顺时针方向旋转 , 得到(点A的对应点为点C),延长交于点F,连接.
(1)、求证:AE平分;(2)、连接BD,求证: .21. 如图1,点E为正方形内一点, , 将绕点B顺时针方向旋转 , 得到(点A的对应点为点C),延长交于点F,连接.
 (1)、试判断四边形的形状,并说明理由;(2)、若 , 如图2,请猜想线段与的数量关系,并加以证明.
(1)、试判断四边形的形状,并说明理由;(2)、若 , 如图2,请猜想线段与的数量关系,并加以证明.