吉林省长春市德惠三中2022-2023学年九年级上学期第一次月考数学试卷
试卷更新日期:2023-11-07 类型:月考试卷
一、选择题(每小题3分,共24分)
-
1. 下列方程中是一元二次方程的是( )A、2x+1=0 B、y2+x=1 C、x2+1=0 D、2. 下列运算中错误的是( )A、 B、 C、 D、3. 以下二次根式:① ;② ;③ ;④ 中,与 是同类二次根式的是( )A、①和② B、②和③ C、①和④ D、③和④4. 若a是方程2x2﹣x﹣3=0的一个解,则6a2﹣3a的值为( )A、3 B、﹣3 C、9 D、﹣95. 若1<x<2,则 的值为( )A、2x﹣4 B、﹣2 C、4﹣2x D、26. 若关于x的方程x2-3x+q=0的一个根x1的值是2.则另一根x2及q的值分别是( )A、x2=1,q=2 B、x2=-1,q=2 C、x2=1,q=-2 D、x2=-1,q=-27. 若α,β是方程x2-2x-3=0的两个实数根,则α2+β2的值为( )A、10 B、9 C、7 D、58. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、
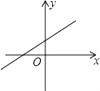 B、
B、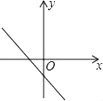 C、
C、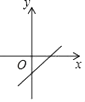 D、
D、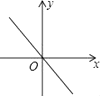
二、填空题(共6小题,每小题3分,满分18分)
-
9. 使有意义的x的取值范围是.10. 若|b-1|+=0,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .11. 在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2 , 根据这个规则,方程(x+2)*5=0的解为 .12. 代数式x2-5x+10的最小值是 .13. 某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为 .
14. 若等腰三角形底边长为8,腰长是方程x2-9x+20=0的一个根,则这个三角形的周长 .三、解答题(共78分)
-
15. 计算:(1)、(2)、16. 解方程(1)、用直接开平方法解 3(x-1)2-6=0;(2)、用配方法解x2-6x+3=0;(3)、用公式法解 9x2+10x=4;(4)、用因式分解法解 2x2-5x=0.17. 先化简,再求值: , 其中x=+1,y=-1.18. 已知关于x的方程(k-1)x2-k2x-1=0的一个根是-1,求k的值;如果方程还有其他的根,请予求出.19. 已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.(1)、求证:方程有两个不相等的实数根;(2)、若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.20. 两个连续奇数的积为255,求这两个奇数.21. 如图,利用一面墙(墙的长度不超过45米),用80米长的篱笆围成一个矩形场地.
①怎样围才能使矩形场地的面积为750平方米?
②能否围成面积为810平方米的矩形场地,为什么?
 22. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,2012年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)、求每年市政府投资的增长率;(2)、若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.23. 某网店销售台灯,成本为每盏30元.销售大数据分析表明:当每盏台灯售价为40元时,平均每月售出600盏,若售价每下降1元,其月销售量就增加200盏.为迎接“双十一”,该网店决定降价促销,在库存为1210盏台灯的情况下,若预计月获利恰好为8400元,求每盏台灯的售价.24. 已知:如图所示.在△ABC中,∠B=90°,AB=5cm , BC=7cm . 点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
22. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,2012年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)、求每年市政府投资的增长率;(2)、若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.23. 某网店销售台灯,成本为每盏30元.销售大数据分析表明:当每盏台灯售价为40元时,平均每月售出600盏,若售价每下降1元,其月销售量就增加200盏.为迎接“双十一”,该网店决定降价促销,在库存为1210盏台灯的情况下,若预计月获利恰好为8400元,求每盏台灯的售价.24. 已知:如图所示.在△ABC中,∠B=90°,AB=5cm , BC=7cm . 点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动. (1)、如果P , Q分别从A , B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P , Q分别从A , B同时出发,那么几秒后,PQ的长度等于5cm?(3)、在(1)中,△PQB的面积能否等于7cm2?说明理由.
(1)、如果P , Q分别从A , B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P , Q分别从A , B同时出发,那么几秒后,PQ的长度等于5cm?(3)、在(1)中,△PQB的面积能否等于7cm2?说明理由.