浙江省杭州重点中学2023-2024学年九年级(上)数学开学试卷
试卷更新日期:2023-11-07 类型:开学考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 若二次根式在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 已知的半径是 , 则中最长的弦长是( )A、 B、 C、 D、3. 如图,菱形中,分别是的中点,若菱形的周长为 , 则的长为( )
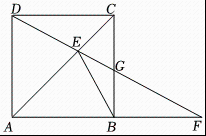
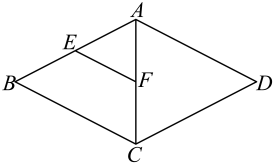 A、 B、 C、 D、4. 某班共有名学生,体育课上老师统计全班一分钟仰卧起坐的个数,由于小亮没有参加此次集体测试,因此计算其他名学生一分钟仰卧起坐的平均个数为个,方差为后来小亮进行了补测,成绩为个,关于该班名学生的一分钟仰卧起坐个数,下列说法正确的是( )A、平均个数不变,方差不变 B、平均个数变小,方差不变 C、平均个数变大,方差变大 D、平均个数不变,方差变小5. 已知二次函数 , 则下列关于这个函数的图象和性质的说法错误的是( )A、图象的开口向下 B、与轴有个交点 C、当时,随的增大而减小 D、对称轴是直线6. 若点 , , , 都在反比例函数为常数,的图象上,其中 , 则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为( )
A、 B、 C、 D、4. 某班共有名学生,体育课上老师统计全班一分钟仰卧起坐的个数,由于小亮没有参加此次集体测试,因此计算其他名学生一分钟仰卧起坐的平均个数为个,方差为后来小亮进行了补测,成绩为个,关于该班名学生的一分钟仰卧起坐个数,下列说法正确的是( )A、平均个数不变,方差不变 B、平均个数变小,方差不变 C、平均个数变大,方差变大 D、平均个数不变,方差变小5. 已知二次函数 , 则下列关于这个函数的图象和性质的说法错误的是( )A、图象的开口向下 B、与轴有个交点 C、当时,随的增大而减小 D、对称轴是直线6. 若点 , , , 都在反比例函数为常数,的图象上,其中 , 则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , , 则的长为( )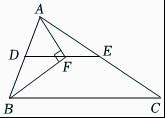 A、 B、 C、 D、8. 关于的一元二次方程有实数根,则的取值范围是( )A、且 B、 C、 D、且9. 当时,二次函数的最小值为 , 则的值为( )A、 B、 C、或 D、或10. 已知二次函数 , 当时,的取值范围是下列结论:
A、 B、 C、 D、8. 关于的一元二次方程有实数根,则的取值范围是( )A、且 B、 C、 D、且9. 当时,二次函数的最小值为 , 则的值为( )A、 B、 C、或 D、或10. 已知二次函数 , 当时,的取值范围是下列结论:对称轴是直线;
;
二次函数的图象经过点 , , 若 , 则;
有最大值 .
其中正确的是( )
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 如图,在中的半径 , 圆心到弦的距离为 , 则弦的长度为 .
 12. 若平行四边形中两个内角的度数比为: , 则其中较大角的度数是 .13. 如图,已经二次函数的图象如图所示,直线轴,则当时的取值范围 .
12. 若平行四边形中两个内角的度数比为: , 则其中较大角的度数是 .13. 如图,已经二次函数的图象如图所示,直线轴,则当时的取值范围 .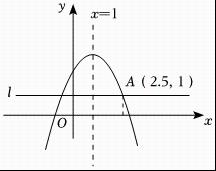 14. 已知关于的二次函数 , 无论取何值,函数图象恒过定点 , 则点的坐标为 .15. 如图,在平面直角坐标系中,的边在轴正半轴上,其中 , 点为斜边的中点,反比例函数的图象过点且交线段于点 , 连结、 , 若 , 则的值为 .
14. 已知关于的二次函数 , 无论取何值,函数图象恒过定点 , 则点的坐标为 .15. 如图,在平面直角坐标系中,的边在轴正半轴上,其中 , 点为斜边的中点,反比例函数的图象过点且交线段于点 , 连结、 , 若 , 则的值为 . 16. 如图,在纸片中, , , , 点 , 分别在、边上,连接 , 将沿翻折,使点落在点的位置,且四边形是菱形.
16. 如图,在纸片中, , , , 点 , 分别在、边上,连接 , 将沿翻折,使点落在点的位置,且四边形是菱形.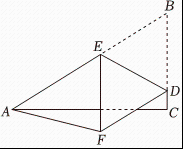 (1)、若点在边上时,则菱形的边长为;(2)、连接 , 则的长的最小值为 .
(1)、若点在边上时,则菱形的边长为;(2)、连接 , 则的长的最小值为 .三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算:;(2)、解方程: .18. 张明和李亮在体育运动中报名参加了百米训练小组在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数
中位数
方差
张明
李亮
 (1)、求张明成绩的平均数和李亮成绩的中位数;(2)、现在从张明和李亮中选择一名成绩比较稳定的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.19. 如图,在▱中,对角线 , 相交于点 , 于点 , 于点 , .
(1)、求张明成绩的平均数和李亮成绩的中位数;(2)、现在从张明和李亮中选择一名成绩比较稳定的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.19. 如图,在▱中,对角线 , 相交于点 , 于点 , 于点 , .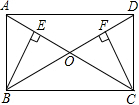 (1)、求证:▱是矩形.(2)、若 , , 求的长.20. 已知一次函数 的图象与反比例函数 图象交于 , 两点,且 点的横坐标 ,求:
(1)、求证:▱是矩形.(2)、若 , , 求的长.20. 已知一次函数 的图象与反比例函数 图象交于 , 两点,且 点的横坐标 ,求: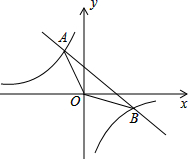 (1)、反比例函数的解析式.(2)、 的面积.(3)、直接写出满足 时 的取值范围.21. 某超市销售一款洗手液,这款洗手液成本价为每瓶元,当销售单价定为每瓶元时,每天可售出瓶.市场调查反应:销售单价每上涨元,则每天少售出瓶.若设这款洗手液的销售单价上涨元,每天的销售量利润为元.(1)、写出每天的销售量,每瓶洗手液的利润;用含的代数式表示(2)、若这款洗手液的日销售利润达到元,则销售单价应上涨多少元?(3)、当销售单价上涨多少元时,这款洗手液每天的销售利润最大,最大利为多少元?
(1)、反比例函数的解析式.(2)、 的面积.(3)、直接写出满足 时 的取值范围.21. 某超市销售一款洗手液,这款洗手液成本价为每瓶元,当销售单价定为每瓶元时,每天可售出瓶.市场调查反应:销售单价每上涨元,则每天少售出瓶.若设这款洗手液的销售单价上涨元,每天的销售量利润为元.(1)、写出每天的销售量,每瓶洗手液的利润;用含的代数式表示(2)、若这款洗手液的日销售利润达到元,则销售单价应上涨多少元?(3)、当销售单价上涨多少元时,这款洗手液每天的销售利润最大,最大利为多少元?