浙江省杭州市临平区2023-2024学年七年级上册数学10月月考试卷
试卷更新日期:2023-11-07 类型:月考试卷
一、选择题(每小题3分,共30分)。
-
1. 利用直角三角板,作的高线,下列作法正确的是( )A、
 B、
B、 C、
C、 D、
D、 2. 式子:①3<5;②4x+5>0;③x=3;④x2+x;⑤x≠4;⑥x+2≥x+1.其中是不等式的有( )A、2个 B、3个 C、4个 D、5个3. 如图是用尺规作∠AOB的平分线OC的示意图,这样作图的依据是( )
2. 式子:①3<5;②4x+5>0;③x=3;④x2+x;⑤x≠4;⑥x+2≥x+1.其中是不等式的有( )A、2个 B、3个 C、4个 D、5个3. 如图是用尺规作∠AOB的平分线OC的示意图,这样作图的依据是( ) A、SAS B、SSS C、ASA D、AAS4. 对于命题“如果a2>b2 , 那么a>b”,下面四组关于a , b的值中,能说明这个命题是假命题的是( )A、a=3,b=-2 B、a=-2,b=3 C、a=3,b=2 D、a=-3,b=25. 已知a>b , 则下列各式中一定成立的是( )A、a-b<0 B、 C、ac2>bc2 D、2a-1<2b-16. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
A、SAS B、SSS C、ASA D、AAS4. 对于命题“如果a2>b2 , 那么a>b”,下面四组关于a , b的值中,能说明这个命题是假命题的是( )A、a=3,b=-2 B、a=-2,b=3 C、a=3,b=2 D、a=-3,b=25. 已知a>b , 则下列各式中一定成立的是( )A、a-b<0 B、 C、ac2>bc2 D、2a-1<2b-16. 如图,在中, , 是的高线,是的角平分线,则的度数是( )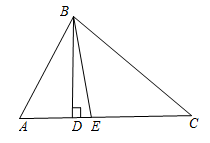 A、 B、 C、 D、7. 如图,已知 , , , 则的度数为( )
A、 B、 C、 D、7. 如图,已知 , , , 则的度数为( ) A、 B、 C、 D、8. 设“〇”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“〇”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( )
A、 B、 C、 D、8. 设“〇”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“〇”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( ) A、〇□△ B、〇△□ C、□〇△ D、△□〇9. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、10. 若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是( )A、-6 B、-5 C、-3 D、-2
A、〇□△ B、〇△□ C、□〇△ D、△□〇9. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、10. 若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是( )A、-6 B、-5 C、-3 D、-2二、填空题(每小题4分,共24分)。
-
11. 三角形三边长为7、12、a,则a的取值范围是 .12. 把命题“线段垂直平分线上的点到这条线段的两个端点的距离相等”改写成“如果…,那么….”的形式 .13. 如图,BD垂直平分垂直平分AF于 , 若 , 则的周长为.
 14. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>94”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 .
14. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>94”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 . 15. 如图,中,E为边上一点, , 点D为的中点,连接 , 取的中点F,连接 , 若四边形的面积是6,则的面积是 .
15. 如图,中,E为边上一点, , 点D为的中点,连接 , 取的中点F,连接 , 若四边形的面积是6,则的面积是 . 16. 邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是元.
16. 邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是元.三、解答题(本题有7小题,共66分)。
-
17.
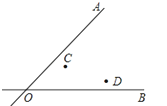
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
 18. 解下列不等式(组):(1)、2x-1>x-3;(2)、 .19. 如图,在△ABC中,BO平分∠ABC , CO平分∠ACB , 过点O作BC的平行线与AB , AC分别相交于点M , N . 若AB=5,AC=6,求△AMN的周长.
18. 解下列不等式(组):(1)、2x-1>x-3;(2)、 .19. 如图,在△ABC中,BO平分∠ABC , CO平分∠ACB , 过点O作BC的平行线与AB , AC分别相交于点M , N . 若AB=5,AC=6,求△AMN的周长.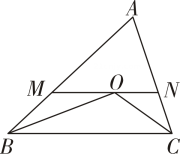 20. 已知:关于的方程组的解为负数,求的取值范围.21. 如图,点 , , 在一条直线上,、均为等边三角形,连接和 , 分别交 , 于点 , , 交于点 .
20. 已知:关于的方程组的解为负数,求的取值范围.21. 如图,点 , , 在一条直线上,、均为等边三角形,连接和 , 分别交 , 于点 , , 交于点 .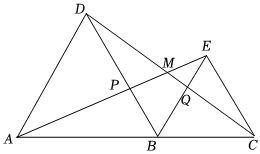 (1)、求证:≌;(2)、求的度数.22. 一群女生住 间宿舍,每间住4人,剩下18人无房住,每间住6人,有一间宿舍住不满,但有学生住.(1)、用含 的代数式表示女生人数.(2)、根据题意,列出关于 的不等式组,并求不等式组的解集.(3)、根据(2)的结论,问一共可能有多少间宿舍,多少名女生?23. 根据以下素材,探索完成任务.
(1)、求证:≌;(2)、求的度数.22. 一群女生住 间宿舍,每间住4人,剩下18人无房住,每间住6人,有一间宿舍住不满,但有学生住.(1)、用含 的代数式表示女生人数.(2)、根据题意,列出关于 的不等式组,并求不等式组的解集.(3)、根据(2)的结论,问一共可能有多少间宿舍,多少名女生?23. 根据以下素材,探索完成任务.如何确定箭头形指示牌?
素材1
某校计划在校园里立一块如图1所示的指示牌,图2为其平面设计图.该指示牌是轴对称图形,由长方形EFHD和三角形ABC组成,且点B,F,E,C四点共线.小聪测量了点A到DH的距离为2.7米,DH=0.8米,DE=1.5米.

素材2
因考虑牢固耐用,小聪打算选用甲、乙两种材料分别制作长方形与三角形(两种图形无缝隙拼接),且甲材料的单价为每平方米85元,乙材料的单价为每平方米100元.

问题解决
任务1
推理最大高度
小聪说:“如果我设计的方案中CB长与C,D两点间的距离相等,那么最高点B到地面的距离就是线段DE长”,他的说法对吗?请判断并说明理由.
任务2
确定箭头形指示牌
小聪发现他设计的方案中,制作广告牌的总费用不超过180元,请你确定CE长度的最大值.
24. 已知,在中, , , , 三点都在直线上, .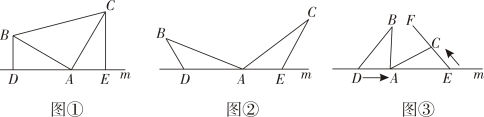 (1)、如图 , 若 , 则与的数量关系为 , , 与的数量关系为 .(2)、如图 , 当不垂直于时,中的结论是否成立?请说明理由.(3)、如图 , 若只保持 , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为是否存在 , 使得与全等?若存在,求出相应的与的值;若不存在,请说明理由.
(1)、如图 , 若 , 则与的数量关系为 , , 与的数量关系为 .(2)、如图 , 当不垂直于时,中的结论是否成立?请说明理由.(3)、如图 , 若只保持 , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为是否存在 , 使得与全等?若存在,求出相应的与的值;若不存在,请说明理由.