浙江省嘉兴市桐乡六中教育集团2023-2024学年九年级(上)数学10月月考试卷
试卷更新日期:2023-11-07 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列事件中,是必然事件的是( )A、任意抛掷一枚硬币,出现正面 B、从2、4、6、8、10这5张卡片中任抽一张是奇数 C、从装有一个红球三个黄球的袋子中任取两球,至少有一个是黄球 D、投掷一枚普通骰子,朝上一面的点数是32. 抛物线与轴的交点坐标是( )A、 B、 C、 D、3. 把抛物线向左平移个单位,所得的新抛物线的函数表达式为( )A、 B、 C、 D、4. 小刚掷一枚均匀的硬币,一连99次都掷出正面朝上,当他第100次掷硬币时,出现正面朝上的概率是( )A、0 B、1 C、 D、5. 若二次函数的图象经过原点,则的值为( )A、 B、 C、或 D、6. 二次函数为常数的部分对应值列表如下:
则代数式的值为( )
A、 B、 C、 D、7. 小明将如图两水平线、的其中一条当成轴,且向右为正方向;两条直线、的其中一条当成轴,且向上为正方向,并在此坐标平面中画出二次函数的图象,则( )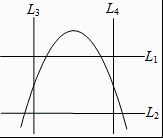 A、为轴,为轴 B、为轴,为轴 C、为轴,为轴 D、为轴,为轴8. 若实数为不大于的非负整数,则使关于的分式方程的解为整数的概率为( )A、 B、 C、 D、9. 某小区有一块绿地如图中等腰直角所示,计划在绿地上建造一个矩形的休闲书吧 , 其中点 , , 分别在边 , , 上,记 , , 图中阴影部分的面积为 , 当在一定范围内变化时,和都随的变化而变化,则与 , 与满足的函数关系分别是( )
A、为轴,为轴 B、为轴,为轴 C、为轴,为轴 D、为轴,为轴8. 若实数为不大于的非负整数,则使关于的分式方程的解为整数的概率为( )A、 B、 C、 D、9. 某小区有一块绿地如图中等腰直角所示,计划在绿地上建造一个矩形的休闲书吧 , 其中点 , , 分别在边 , , 上,记 , , 图中阴影部分的面积为 , 当在一定范围内变化时,和都随的变化而变化,则与 , 与满足的函数关系分别是( )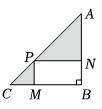 A、一次函数关系,二次函数关系 B、一次函数关系,反比例函数关系 C、二次函数关系,一次函数关系 D、反比例函数关系,二次函数关系10. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”,已知点 , 有下列结论:
A、一次函数关系,二次函数关系 B、一次函数关系,反比例函数关系 C、二次函数关系,一次函数关系 D、反比例函数关系,二次函数关系10. 定义:在平面直角坐标系中,对于点 , 当点满足时,称点是点的“倍增点”,已知点 , 有下列结论:①点 , 都是点的“倍增点”;
②若直线上的点A是点的“倍增点”,则点的坐标为;
③抛物线上存在两个点是点的“倍增点”;
④若点是点的“倍增点”,则的最小值是 .
其中,正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题(本大题共6小题,共18.0分)
-
11. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .12. 已知点 , , 在二次函数的图象上,则 , , 的大小关系是用“”连接 .13. 若将二次函数配方为的形式,则y=。14. 二次函数图象如图,下列结论中:;;;正确的有填序号
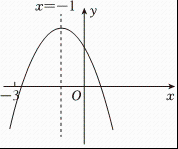 15. 坐标平面上有两个二次函数的图象,其顶点 , 均在轴上,且有一条水平线与两图象相交于 , , , 四点,各点位置如图所示,若 , , , 则的长度为 .
15. 坐标平面上有两个二次函数的图象,其顶点 , 均在轴上,且有一条水平线与两图象相交于 , , , 四点,各点位置如图所示,若 , , , 则的长度为 . 16. 已知二次函数(1)、若 , 则函数的最小值为 .(2)、若当时,的最大值是 , 则的值为 .
16. 已知二次函数(1)、若 , 则函数的最小值为 .(2)、若当时,的最大值是 , 则的值为 .三、解答题(本大题共8小题,共52.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌上,随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字.(1)、能组成哪些两位数?(请用树状图表示出来)(2)、恰好是偶数的概率是多少?18. 如图,、两点在一次函数与二次函数的图象上
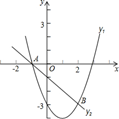 (1)、求一次函数和二次函数的解析式;(2)、请直接写出时,自变量的取值范围.19. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中.
(1)、求一次函数和二次函数的解析式;(2)、请直接写出时,自变量的取值范围.19. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为12m.现将它的图形放在如图所示的直角坐标系中. (1)、求这条抛物线的解析式.(2)、一艘宽为4米,高出水面3米的货船,能否从桥下通过?20. 一个不透明口袋中装有红球个,黄球个,绿球个,这些球除颜色处没有任何其他区别现.从中任意摸出一个球.(1)、计算摸到的是绿球的概率.(2)、如果要使摸到绿球的概率为 , 需要在这个口袋中再放入多少个绿球?21. 已知二次函数(m为常数).(1)、求证:函数与轴有两个交点;(2)、若当时,随的增大而增大,求的取值范围.22. 某市林业局积极响应习总书记“青山绿水就是金山银山”的号召,特地考察一种花卉移植的成活率,对本市这种花卉移植成活的情况进行了调查统计,并绘制了如图所示的统计图.
(1)、求这条抛物线的解析式.(2)、一艘宽为4米,高出水面3米的货船,能否从桥下通过?20. 一个不透明口袋中装有红球个,黄球个,绿球个,这些球除颜色处没有任何其他区别现.从中任意摸出一个球.(1)、计算摸到的是绿球的概率.(2)、如果要使摸到绿球的概率为 , 需要在这个口袋中再放入多少个绿球?21. 已知二次函数(m为常数).(1)、求证:函数与轴有两个交点;(2)、若当时,随的增大而增大,求的取值范围.22. 某市林业局积极响应习总书记“青山绿水就是金山银山”的号召,特地考察一种花卉移植的成活率,对本市这种花卉移植成活的情况进行了调查统计,并绘制了如图所示的统计图.请你根据统计图提供的信息,回答下列问题:
 (1)、这种花卉成活的频率稳定在附近,估计成活概率为精确到(2)、该林业局已经移植这种花卉棵.
(1)、这种花卉成活的频率稳定在附近,估计成活概率为精确到(2)、该林业局已经移植这种花卉棵.估计这批花卉成活的棵数;
根据市政规划共需要成活棵这种花卉,估计还需要移植多少棵?
23. 某企业准备对A , B两个生产性项目进行投资,根据其生产成本、销售情况等因素进行分析得知:投资A项目一年后的收益(万元)与投入资金x(万元)的函数表达式为: , 投资B项目一年后的收益(万元)与投入资金x(万元)的函数表达式为: .(1)、若将10万元资金投入A项目,一年后获得的收益是多少?(2)、若对A , B两个项目投入相同的资金m()万元,一年后两者获得的收益相等,则m的值是多少?(3)、2023年,我国对小微企业施行所得税优惠政策.该企业将根据此政策获得的减免税款及其他结余资金共计32万元,全部投入到A , B两个项目中,当A , B两个项目分别投入多少万元时,一年后获得的收益之和最大?最大值是多少万元?24. 抛物线与轴交于点和点 , 与轴交于点 , 点为第一象限内抛物线上的动点,过点作轴于点 , 交于点 .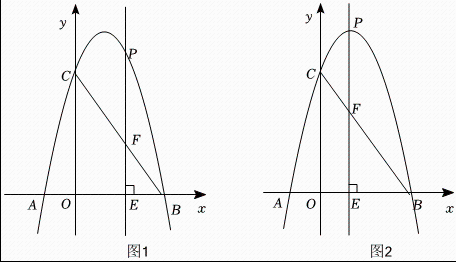 (1)、求抛物线的解析式;(2)、如图 , 当线段长度是线段长度的倍时,求点的横坐标;(3)、如图 , 当点运动到抛物线顶点时,点是轴上的动点,连接 , 过点作直线 , 连接并延长交直线于点 , 当时,请直接写出点的坐标.
(1)、求抛物线的解析式;(2)、如图 , 当线段长度是线段长度的倍时,求点的横坐标;(3)、如图 , 当点运动到抛物线顶点时,点是轴上的动点,连接 , 过点作直线 , 连接并延长交直线于点 , 当时,请直接写出点的坐标.