广东省广州大学附中2023-2024学年九年级（上）数学10月月考试卷

试卷更新日期：2023-11-07 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将一元二次方程 $5 x^{2} - 1 = 4 x$ 化成一般形式后，二次项的系数和一次项系数分别是（）

A、 $5$ ， $- 1$ B、 $5$ ， $4$ C、 $5$ ， $- 4$ D、 $5$ ， $1$

查看试题解析
3. 抛物线 $y = - (x - 2)^{2} + 3$ 的顶点坐标是（）

A、 $(- 2 ， 3)$ B、 $(2 ， 3)$ C、 $(2 ， - 3)$ D、 $(- 2 ， - 3)$

查看试题解析
4. 参加足球联赛的每两队之间都进行两场比赛，共要比赛 $90$ 场，设共有 $x$ 个队参加比赛，则下列方程符合题意的是（）

A、 $\frac{1}{2} x (x + 1) = 90$ B、 $x (x + 1) = 90$ C、 $\frac{1}{2} x (x - 1) = 90$ D、 $x (x - 1) = 90$

查看试题解析
5. 若二次函数 $y = (a - 1) x^{2} + 3 x + a^{2} - 1$ 的图象经过原点，则 $a$ 的值必为（）

A、 $1$ 或 $- 1$ B、 $1$ C、 $- 1$ D、 $0$

查看试题解析
6. 若关于 $x$ 的方程 $m x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m < - 1$ B、 $m > - 1$ 且 $m \neq 0$ C、 $m > - 1$ D、 $m \geq - 1$ 且 $m \neq 0$

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 40 °$ ，点D，P分别是图中所作直线和射线与 $A B$ ， $C D$ 的交点.根据图中尺规作图痕迹推断，以下结论错误的是（）

A、 $A D = C D$ B、 $∠ A B P = ∠ C B P$ C、 $∠ B P C = 115 °$ D、 $∠ P B C = ∠ A$

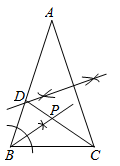查看试题解析
8. 已知一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1}^{2} - 5 x_{1} - 2 x_{2}$ 的值为（）

A、 $- 7$ B、 $- 3$ C、 $2$ D、 $5$

查看试题解析
9. 某餐厅主营盒饭业务，每份盒饭的成本为 $12$ 元.若每份盒饭的售价为 $16$ 元，每天可卖出 $360$ 份.市场调查反映：如调整价格，每涨价 $1$ 元，每天要少卖出 $40$ 份.若该餐厅想让每天盒饭业务的利润达到 $1680$ 元，设每份盒饭涨价 $x$ 元，则符合题意的方程是（）

A、 $(16 + x - 12) (360 - 40 x) = 1680$ B、 $(x - 12) (360 - 40 x) = 1680$ C、 $(x - 12) [360 - 40 (x - 16)] = 1680$ D、 $(16 + x - 12) [360 - 40 (x - 16)] = 1680$

查看试题解析
10. 抛物线上 $y = (m - 4) x^{2}$ 有两点 $A (- 3 ， y_{1})$ 、 $B (2 ， y_{2})$ ，且 $y_{1} > y_{2}$ ，则 $m$ 的取值范围是（）

A、 $m > 4$ B、 $m < 4$ C、 $m \geq 4$ D、 $m \neq 4$

查看试题解析

二、填空题（本大题共6小题，共18.0分）

11. 一元二次方程 $x^{2} - 3 x + 2 = 0$ 根的判别式 $Δ =$ ．

查看试题解析
12. 在函数 $y = \frac{\sqrt{x - 2}}{x - 3}$ 中，自变量的取值范围是．

查看试题解析
13. 若二次函数 $y = a x^{2} + b x - 1$ 经过 $(- 1 ， 0)$ ，则 $2023 + 2 a - 2 b$ 的值为．

查看试题解析
14. 化简： $\frac{2 a - 2}{a^{2} - 4 a + 4} \div \frac{a - 1}{a - 2} =$ ．

查看试题解析
15. 如图，四边形 $A B C D$ 中的两条对角线 $A C$ ， $B D$ 互相垂直， $A C + B D = 10$ ，当 $A C$ 为时．四边形 $A B C D$ 的面积最大．

查看试题解析
16. 如图，平面内三点 $A$ 、 $B$ 、 $C$ ， $A B = 4$ ， $A C = 3$ ，以 $B C$ 为对角线作正方形 $B D C E$ ，连接 $A D$ ，则 $A D$ 的最大值是．

查看试题解析

三、计算题（本大题共1小题，共4.0分）

17. 用适当的方法解方程．

(1)、 $4 (x - 1)^{2} = 9$ ．

(2)、 $x^{2} - 6 x - 4 = 0$ ．

查看试题解析

四、解答题（本大题共8小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

18. 如图，要设计一本书的封面，封面长为 $27 c m$ ，宽为 $21 c m$ ，正中央是一个与整个封面长宽比例相同的矩形 $.$ 如果要使四周的彩色边衬所占面积是封面面积的 $\frac{1}{4}$ ，上下边衬等宽，左右边衬等宽，应如何设计四周的宽度 $($ 结果保留根号 $)$ ？

查看试题解析
19. 一名男生推铅球，铅球行进高度 $y$ （单位： $m$ ）与水平距离 $x$ （单位： $m$ ）之间的函数关系是 $y = - \frac{1}{12} {(x - 4)}^{2} + 3$ .如图， $A$ ， $B$ 是该函数图象上的两点.

(1)、画出该函数的大致图象；

(2)、请判断铅球推出的距离能否达到 $11 m$ ，并说明理由.

查看试题解析
20. 已知：a是不等式 $5 (a - 2) + 8 < 6 (a - 1) + 7$ 的最小整数解，请用配方法解关于x的方程 $x^{2} + 2 a x + a + 1 = 0$ .

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 m x + 3 m^{2} = 0$ ．

(1)、求证：该方程总有两个实数根；

(2)、若 $m > 0$ ，且该方程的两个实数根的差为2，求 $m$ 的值．

查看试题解析
22. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (1 ， 0)$ 和 $B (- 3 ， 0)$ ，与 $y$ 轴交于 $C (0 ， 3)$ ．

(1)、求抛物线的解析式，并求出顶点 $D$ 的坐标．

(2)、观察图象，直接写出一元二次不等式： $a x^{2} + b x + c < 0$ 解集为：

(3)、若抛物线的对称轴交 $x$ 轴于点 $M$ ，求四边形 $B M C D$ 的面积．

查看试题解析
23. 如图，抛物线 $y = a (x + 1)^{2}$ 的顶点为 $A$ ，与 $y$ 轴的负半轴交于点 $B$ ，且 $S_{△ A O B} = \frac{1}{2}$ ．

(1)、求抛物线的解析式；

(2)、若点 $C$ 是该抛物线上 $A$ 、 $B$ 两点之间的一点，求 $S_{△ A B C}$ 最大时，点 $C$ 的坐标．

查看试题解析
24. 小爱同学学习二次函数后，对函数 $y = - {(| x | - 1)}^{2}$ 进行了探究．在经历列表、描点、连线步骤后，得到如图的函数图象．请根据函数图象，回答下列问题：

(1)、观察探究：
$①$ 写出该函数的一条性质：；
$②$ 方程 $- {(| x | - 1)}^{2} = - 1$ 的解为：；
$③$ 若方程 $- {(| x | - 1)}^{2} = m$ 有四个实数根，则 $m$ 的取值范围是．

(2)、延伸思考：
将函数 $y = - {(| x | - 1)}^{2}$ 的图象经过怎样的平移可得到函数 $y_{1} =^{- {(| x - 1 | - 1)}^{2} + 2}$ 的图象？写出平移过程，并直接写出当 $1 < y_{1} \leq 2$ 时，自变量 $x$ 的取值范围．

查看试题解析
25.

(1)、问题背景：如图 $1$ ， $△ A C B$ 和 $△ C E F$ 都是等腰直角三角形，点 $E$ 在 $A B$ 上，连 $B F$ ，求证： $B F ⊥ A B$ ；

(2)、迁移运用：如图 $2$ ，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ，点 $P$ 在 $△ A B C$ 外， $P A = 2$ ， $P B = 6$ ， $∠ B P A = 60 °$ ，求 $P C$ 的长；

(3)、拓展提升：如图 $3$ ，在等腰 $R t △ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点 $E$ 、 $F$ 在 $△ A B C$ 外， $∠ E C F = 135 °$ ， $B E / / A F$ ，直接写出线段 $B E$ 、 $A F$ 、 $E F$ 之间的关系．

查看试题解析