广东省广州市越秀区重点中学2023-2024学年八年级(上)数学10月段考试卷
试卷更新日期:2023-11-07 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 数学考试必备学习用具:黑色的水笔。2B铅笔、橡皮、圆规、三角板全套、量角器.下列学习用具所抽象出的几何图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个三角形两边长分别为和 , 则此三角形的第三边的长可能是( )A、 B、 C、 D、3. 平面直角坐标系中,点关于轴的对称点的坐标是( )A、 B、 C、 D、4. 小明在所面对的平面镜内看到他背后墙上时钟所成的像如图所示,则此时的实际时刻应是( )
2. 一个三角形两边长分别为和 , 则此三角形的第三边的长可能是( )A、 B、 C、 D、3. 平面直角坐标系中,点关于轴的对称点的坐标是( )A、 B、 C、 D、4. 小明在所面对的平面镜内看到他背后墙上时钟所成的像如图所示,则此时的实际时刻应是( ) A、: B、: C、: D、:5. 如图,≌ , , , , 则为( )
A、: B、: C、: D、:5. 如图,≌ , , , , 则为( ) A、 B、 C、 D、6. 如图,射线平分 , 点、分别在射线、上,若 , 的面积为 , 过点作于点 , 则的长为( )
A、 B、 C、 D、6. 如图,射线平分 , 点、分别在射线、上,若 , 的面积为 , 过点作于点 , 则的长为( ) A、 B、 C、 D、7. 如图, , , 三个居民小区的位置成三角形,现决定在三个小区之间修建一个超市,使它到三个小区的距离相等,则超市应建在( )
A、 B、 C、 D、7. 如图, , , 三个居民小区的位置成三角形,现决定在三个小区之间修建一个超市,使它到三个小区的距离相等,则超市应建在( ) A、 , 的两条高线的交点处 B、 , 两内角平分线的交点处 C、 , 两边中线的交点处 D、 , 两条边垂直平分线的交点处8. 多边形的内角和为 , 那么从这个多边形的一个顶点引出的对角线的条数是( )A、条 B、条 C、条 D、条9. 如图,在Rt△ABC中, , , 分别以边A、B为圆心,大于的长为半径画弧,两弧分别交于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若 , 则BC的长为( ).
A、 , 的两条高线的交点处 B、 , 两内角平分线的交点处 C、 , 两边中线的交点处 D、 , 两条边垂直平分线的交点处8. 多边形的内角和为 , 那么从这个多边形的一个顶点引出的对角线的条数是( )A、条 B、条 C、条 D、条9. 如图,在Rt△ABC中, , , 分别以边A、B为圆心,大于的长为半径画弧,两弧分别交于F、G两点,连接F、G分别交于AB于E、BC于D,连接AD,若 , 则BC的长为( ).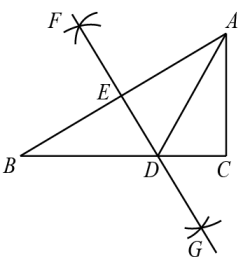 A、6 B、 C、9 D、10. 如图,在中,内角与外角的平分线相交于点 , , 在延长线上,交于 , 交于 , 连接下列结论:;::;垂直平分;; , 其中正确的有( )
A、6 B、 C、9 D、10. 如图,在中,内角与外角的平分线相交于点 , , 在延长线上,交于 , 交于 , 连接下列结论:;::;垂直平分;; , 其中正确的有( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 正十边形有条对称轴.12. 如果等腰三角形两边长是6cm和3cm,那么它的周长是 cm.13. 如图所示,将长方形纸条的一角沿虚线折叠,平分 , 则 .
 14. 如图,在中, , , 则的度数是
14. 如图,在中, , , 则的度数是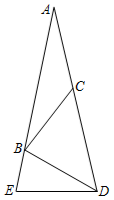 15. 上午时,一条船从港口出发,以海里时的速度向正北方向航行,时到达海岛处,从 , 两处望灯塔 , 分别测得 , 若该船从海岛继续向正北航行,则船与灯塔的最短距离为 .
15. 上午时,一条船从港口出发,以海里时的速度向正北方向航行,时到达海岛处,从 , 两处望灯塔 , 分别测得 , 若该船从海岛继续向正北航行,则船与灯塔的最短距离为 .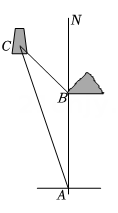 16. 如图,平面直角坐标系中,点 , 分别在轴,轴的负半轴上, , 且交轴于点、交轴于点 , 若平分 , 则线段 , , 之间的数量关系是 .
16. 如图,平面直角坐标系中,点 , 分别在轴,轴的负半轴上, , 且交轴于点、交轴于点 , 若平分 , 则线段 , , 之间的数量关系是 .
三、计算题(本大题共1小题,共10.0分)
-
17. 如图,在中,、分别在、上且 , 平分 , 于点 .
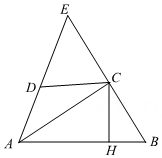 (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.四、解答题(本大题共7小题,共62.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 如图,计划在某小区道路上建一个智能垃圾分类投放点 , 使得道路附近的两栋住宅楼 , 到智能垃圾分类投放点的距离相等请在图中利用尺规作图保留作图痕迹,不写作法 , 确定点的位置.
 19. 在平面直角坐标系中的位置如图所示.
19. 在平面直角坐标系中的位置如图所示.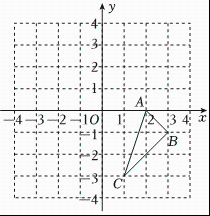 (1)、在图中作出与关于轴对称的 , 并写出 , 的坐标.(2)、在轴上画出点 , 使得的值最小.20. 已知 , 是的角平分线, , , 试求与的度数.
(1)、在图中作出与关于轴对称的 , 并写出 , 的坐标.(2)、在轴上画出点 , 使得的值最小.20. 已知 , 是的角平分线, , , 试求与的度数. 21. 如图,点 , , , 在同一直线上, , , , 求证:≌ .
21. 如图,点 , , , 在同一直线上, , , , 求证:≌ . 22. 如图,Rt△ABE中,∠A=90°,点C在AB上,∠CEB=2∠AEC=45°.
22. 如图,Rt△ABE中,∠A=90°,点C在AB上,∠CEB=2∠AEC=45°.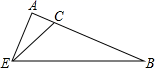 (1)、求∠B的度数;(2)、求证:BC=2AE.23. 如图,在平面直角坐标系中,点 , 点在轴正半轴上,点在轴负半轴上, , 点是轴上的一动点点不与、重合 , , , 连接 .
(1)、求∠B的度数;(2)、求证:BC=2AE.23. 如图,在平面直角坐标系中,点 , 点在轴正半轴上,点在轴负半轴上, , 点是轴上的一动点点不与、重合 , , , 连接 .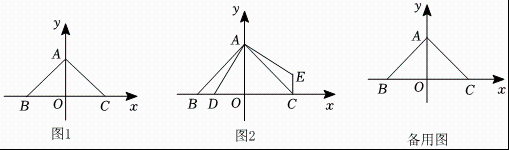 (1)、如图 , 直接写出点 , 的坐标;(2)、如图 , 当点在边上时,求证: , ;(3)、当时,求点的坐标.24. 在等边的两边、所在直线上分别有两点、 , 为外一点,且 , , 探究:当、分别在直线、上移动时,、、之间的数量关系及的周长与等边的周长的关系.
(1)、如图 , 直接写出点 , 的坐标;(2)、如图 , 当点在边上时,求证: , ;(3)、当时,求点的坐标.24. 在等边的两边、所在直线上分别有两点、 , 为外一点,且 , , 探究:当、分别在直线、上移动时,、、之间的数量关系及的周长与等边的周长的关系.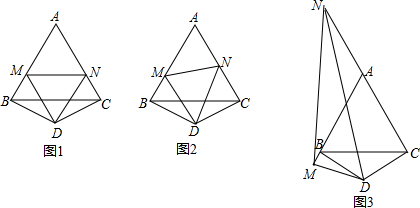 (1)、如图 , 当点、边、上,且时,、、之间的数量关系是;此时;(2)、如图 , 点、边、上,且当时,猜想问的两个结论还成立吗?写出你的猜想并加以证明;(3)、如图 , 当、分别在边、的延长线上时,若 , 则用、表示 .
(1)、如图 , 当点、边、上,且时,、、之间的数量关系是;此时;(2)、如图 , 点、边、上,且当时,猜想问的两个结论还成立吗?写出你的猜想并加以证明;(3)、如图 , 当、分别在边、的延长线上时,若 , 则用、表示 .
-