广东省惠州市惠阳重点中学2023-2024学年九年级（上）数学10月月考试卷

试卷更新日期：2023-11-07 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列各方程中，是一元二次方程的是（）

A、 $x^{2} = 1$ B、 $\frac{1}{x^{2} - 3 x} = 1$ C、 $x^{2} + y^{2} = 1$ D、 $\sqrt{x^{2} + 1} = 1$

查看试题解析
2. 抛物线 $y = 3 x^{2}$ 向右平移1个单位，再向下平移2个单位，所得到的抛物线是（）

A、 $y = 3 {(x - 1)}^{2} - 2$ B、 $y = 3 {(x + 1)}^{2} - 2$ C、 $y = 3 {(x + 1)}^{2} + 2$ D、 $y = 3 {(x - 1)}^{2} + 2$

查看试题解析
3. 下列函数中， $y$ 一定是 $x$ 的二次函数的是（）

A、 $y = - x^{2} + 1$ B、 $y = a x^{2} + b x + c$ C、 $y = 2 x + 3$ D、 $x^{2} y = 1$

查看试题解析
4. 一元二次方程 $2 x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
5. 如图，在一块长为 $22$ 米，宽为 $17$ 米的矩形地面上，要修建同样宽的两条互相垂直的道路 $($ 两条道路各与矩形的一条边平行 $)$ ，剩余部分种上草坪，使草坪面积为 $300$ 平方米．若设道路宽为 $x$ 米，则根据题意可列方程为（）

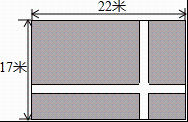A、 $22 \times 17 - 17 x - 22 x = 300$ B、 $22 \times 17 - 17 x - 22 x - x^{2} = 300$ C、 $(22 - x) (17 - x) = 300$ D、 $(22 + x) (17 + x) = 300$

查看试题解析
6. 已知函数 $y = (x - 1)^{2} + 2$ ，当函数值 $y$ 随 $x$ 的增大而减小时， $x$ 的取值范围是（）

A、 $x < 1$ B、 $x > 1$ C、 $x > - 2$ D、 $- 2 < x < 4$

查看试题解析
7. 学校初二年级组织足球联赛，赛制为单循环制（每两个队之间比赛一场).共进行了 $28$ 场比赛，问初二年级有几个参赛班级？设初二年级有 $x$ 个班级参加比赛.根据题意列出方程正确的是（）

A、 $x^{2} = 28$ B、 $\frac{1}{2} x (x - 1) = 28$ C、 $\frac{1}{2} x^{2} = 28$ D、 $x (x - 1) = 28$

查看试题解析
8. 对于函数 $y = - 3 {(x - 1)}^{2}$ 与 $y = - 3 x^{2}$ 的图象的比较，下列说法不正确的是（）

A、开口都向下 B、最大值都为0 C、对称轴相同 D、与x轴都只有一个交点

查看试题解析
9. 设 $m$ 、 $n$ 是一元二次方程 $x^{2} + 2 x - 7 = 0$ 的两个根，则 $m^{2} + 3 m + n =$ （）

A、 $- 5$ B、 $9$ C、 $5$ D、 $7$

查看试题解析
10. 在同一直角坐标系中，一次函数 $y = - a x + b$ 与二次函数 $y = a x^{2} - b$ 的大致图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 一元二次方程x²=4x的根是．

查看试题解析
12. 二次函数 $y = x^{2} - 1$ 图象的顶点坐标是．

查看试题解析
13. 抛物线 $y = (m - 2) x^{2} + 2 x + (m^{2} - 4)$ 的图象经过原点，则 $m =$ ．

查看试题解析
14. 若一元二次方程 $x^{2} + 2 x - 3 = 0$ 的两根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1}^{2} + x_{2}^{2} =$ ．

查看试题解析
15. 有一种流感病毒，刚开始有2人患了流感，经过两轮传染后共有128人患流感.如果设每轮传染中平均一个人传染x个人，那么可列方程为.

查看试题解析
16. 在平面直角坐标系中，抛物线 $y = x^{2}$ 的图象如图所示．已知A点坐标为 $(1 ， 1)$ ，过点A作 $A A_{1} // x$ 轴交抛物线于点 $A_{1}$ ，过点 $A_{1}$ 作 $A_{1} A_{2} // O A$ 交抛物线于点 $A_{2}$ ，过点 $A_{2}$ 作 $A_{2} A_{3} // x$ 轴交抛物线于点 $A_{3}$ ，过点 $A_{3}$ 作 $A_{3} A_{4} // O A$ 交抛物线于点 $A_{4}$ …，依次进行下去，则点 $A_{99}$ 的坐标为．

查看试题解析

三、计算题（本大题共1小题，共6.0分）

17. 解方程

(1)、 $x^{2} - 2 x - 3 = 0$

(2)、 $x (x - 2) + x - 2 = 0$

查看试题解析

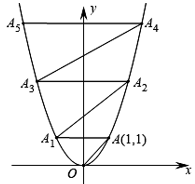
四、解答题（本大题共8小题，共60.0分。解答应写出文字说明，证明过程或演算步骤）

18. 已知 $3$ 是一元二次方程 $x^{2} - 2 x + a = 0$ 的一个根，求 $a$ 的值和方程的另一根．

查看试题解析
19. 已知一抛物线顶点坐标为 $(1 ， 4)$ ，且经过点 $(2 ， 8)$ ，写出该抛物线的对称轴，并求该抛物线的解析式．

查看试题解析
20. 受益于国家支持新能源汽车发展和“带一路”发展战略等多重利好因素，某市某汽车零部件生产企业的利润逐年提高，据统计 $2017$ 年利润为 $2$ 亿元， $2019$ 年利润为 $3.38$ 亿元．

(1)、求该企业从 $2017$ 年到 $2019$ 年利润的年平均增长率；

(2)、若 $2020$ 年保持前两年利润的年平均增长率不变，该企业 $2020$ 年的利润能否超过过 $4$ 亿元？

查看试题解析
21. 如图，某农户准备建一个长方形养鸡场ABCD，养鸡场的一边靠墙，另三边用篱笆围成，若墙长为18 m，墙对面有一个2 m宽的门，篱笆总长为33 m，围成的长方形养鸡场除门之外四周不能有空隙．

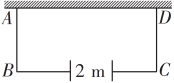(1)、若AB＝x m，则BC＝m；

(2)、要使围成的养鸡场面积为150 m² ，则AB的长为多少？

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} - 2 (m + 1) x + m^{2} + 2 = 0$ ．

(1)、若方程总有两个实数根，求 $m$ 的取值范围；

(2)、若两实数根 $x_{1}$ 、 $x_{2}$ 满足 $(x_{1} + 1) (x_{2} + 1) = 8$ ，求 $m$ 的值．

查看试题解析
23. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 8 c m$ ， $B C = 4 c m$ ，一动点 $P$ 从点 $C$ 出发沿着 $C B$ 方向以 $1 c m / s$ 的速度运动，另一动点 $Q$ 从 $A$ 出发沿着 $A C$ 边以 $2 c m / s$ 的速度运动， $P$ ， $Q$ 两点同时出发，运动时间为 $t (s)$ ．

(1)、若 $△ P C Q$ 的面积是 $△ A B C$ 面积的 $\frac{1}{4}$ ，求 $t$ 的值？

(2)、 $△ P C Q$ 的面积能否为 $△ A B C$ 面积的一半？若能，求出 $t$ 的值；若不能，说明理由．

查看试题解析
24. 某超市经销一种商品，每千克成本为 $30$ 元，经试销发现，该种商品的每天销售量 $y ($ 千克 $)$ 与销售单价 $x ($ 元 $/$ 千克 $)$ 满足一次函数关系，其每天销售单价、销售量的四组对应值如表所示：
销售单价 $x ($ 元 $/$ 千克 $)$
$40$
$45$
$55$
$60$
销售量 $y ($ 千克 $)$
     $80$
     $70$
     $50$
     $40$

(1)、求 $y$ 与 $x$ 之间的函数表达式．

(2)、若商店按不低于成本价，且不高于 $60$ 元的单价销售该商品，要使每天获得的利润为 $800$ 元，求每天的销售量．

(3)、能使销售该商品每天获得的利润为 $1400$ 元吗？若能，销售单价为多少？若不能，请说明理由．

查看试题解析
25. 如图，直线 $y = - 3 x + 3$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、 $B .$ 抛物线 $y = a (x - 2)^{2} + k$ 经过 $A$ 、 $B$ ，并与 $x$ 轴交于另一点 $C$ ，其顶点为 $P$ ，

(1)、求 $a$ ， $k$ 的值；

(2)、抛物线的对称轴上是否存在一点 $M$ ，使 $△ A B M$ 的周长最小？若存在，求 $△ A B M$ 的周长；若不存在，请说明理由；

(3)、抛物线的对称轴是上是否存在一点 $N$ ，使 $△ A B N$ 是以 $A B$ 为斜边的直角三角形？若存在，求出 $N$ 点的坐标，若不存在，请说明理由．

查看试题解析

销售单价 $x ($ 元 $/$ 千克 $)$	$40$	$45$	$55$	$60$
销售量 $y ($ 千克 $)$	$80$	$70$	$50$	$40$