浙江省宁波市鄞州区九年级十二校联考2023-2024学年九年级上学期数学10月月考试卷
试卷更新日期:2023-11-07 类型:月考试卷
一、选择题(本大题有10个小题,每小题3分,共30分.)
-
1. 下列各式中,y是x的二次函数的是( )A、 B、 C、 D、2. 已知⊙O的半径是4,点P在⊙O内,则OP的长可能是( )A、3 B、4 C、4.5 D、53. 已知△ABC∽△DEF , AB=4,DE=8,若△ABC的面积是6,则△DEF的面积是( )A、12 B、16 C、24 D、324. 若(xy≠0),则下列比例式成立的是( )A、 B、 C、 D、5. 在平面直角坐标系中,将抛物线向右平移2个单位,再向下平移4个单位,得到的抛物线的解析式是( )A、 B、 C、 D、6. 如图,将△ABC绕点A逆时针旋转70°,得到△ADE , 若点D在线段BC的延长线上,则∠B的大小是( )
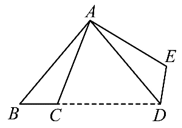 A、45° B、55° C、60° D、100°7. 如图,AB是⊙O的直径,弦AC , BD交于点E , 若弧CD的度数是54°,则∠AED的度数是( )
A、45° B、55° C、60° D、100°7. 如图,AB是⊙O的直径,弦AC , BD交于点E , 若弧CD的度数是54°,则∠AED的度数是( )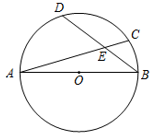 A、54° B、60° C、63° D、72°8. 如图,△ABC的中线BD , CE交于点F , 连结DE , 则S△ADE:S△DEF=( )
A、54° B、60° C、63° D、72°8. 如图,△ABC的中线BD , CE交于点F , 连结DE , 则S△ADE:S△DEF=( )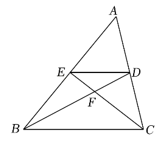 A、2:1 B、4:1 C、5:2 D、3:19. 已知:点 , , 都在抛物线上,则的大小关系是( )A、 B、 C、 D、10. 如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC
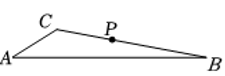
A、2:1 B、4:1 C、5:2 D、3:19. 已知:点 , , 都在抛物线上,则的大小关系是( )A、 B、 C、 D、10. 如图,在△ABC纸板中,AC=4,BC=8,AB=10,P是BC上一点,沿过点P的直线剪下一个与△ABC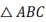 相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )
相似的小三角形纸板.针对CP的不同取值,三人的说法如下.下列判断正确的是( )甲:若CP=4,则有3种不同的剪法;乙:若CP=2,则有4种不同的剪法;
丙:若CP=1,则有3种不同的剪法.
 A、只有甲错 B、只有乙错 C、只有丙错 D、甲、乙、丙都对
A、只有甲错 B、只有乙错 C、只有丙错 D、甲、乙、丙都对二、填空题(本大题有6个小题,每小题4分,共24分.)
-
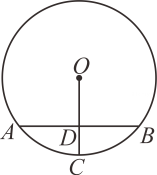
11. 二次函数的顶点坐标是 .12. 若 , 则的值为 .13. 如图,AB是⊙O的弦,C是的中点,OC交AB于点D . 若AB=8cm,CD=2cm,则⊙O的半径为cm.
 14. 如图,7个边长为1的正方形拼成一个长方形,连结AC和BD交正方形边长于点E , F , 则EF的长是 .
14. 如图,7个边长为1的正方形拼成一个长方形,连结AC和BD交正方形边长于点E , F , 则EF的长是 .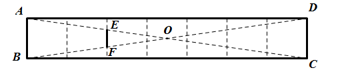 15. 二次函数的图象经过点(1,-1),则a+b的值等于 , 设该函数的顶点为 , 则的最大值等于.16. 如图,在△ABC中,AB=AC=m , D为BC的中点,BD=n , E , F分别在AB , AC上,若∠EDF=90°-∠A , 则△AEF的周长是.(用含m , n的代数式表示)
15. 二次函数的图象经过点(1,-1),则a+b的值等于 , 设该函数的顶点为 , 则的最大值等于.16. 如图,在△ABC中,AB=AC=m , D为BC的中点,BD=n , E , F分别在AB , AC上,若∠EDF=90°-∠A , 则△AEF的周长是.(用含m , n的代数式表示)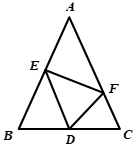
三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤.)
-
17. 已知抛物线经过点(-2,0),(6,0)
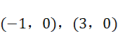 . (1)、求该抛物线的对称轴.(2)、自变量x在什么范围内时,y随x的增大而减小?18. 如图,AB是⊙O的直径,C , D在⊙O上,且位于AB异侧,弧BC , 弧AD的度数分别为60°,100°,请仅用直尺按要求作图.
. (1)、求该抛物线的对称轴.(2)、自变量x在什么范围内时,y随x的增大而减小?18. 如图,AB是⊙O的直径,C , D在⊙O上,且位于AB异侧,弧BC , 弧AD的度数分别为60°,100°,请仅用直尺按要求作图.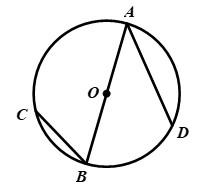 (1)、画出一个大小为30°的角,并写出该角.(2)、画出一个以AD为腰的等腰三角形,并写出该等腰三角形.19. 已知:如图,△ABC
(1)、画出一个大小为30°的角,并写出该角.(2)、画出一个以AD为腰的等腰三角形,并写出该等腰三角形.19. 已知:如图,△ABC 中,AB=2,BC=4,D为BC边上一点,BD=1.
中,AB=2,BC=4,D为BC边上一点,BD=1.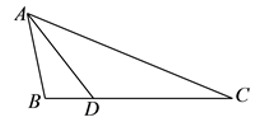 (1)、求证:△ABD∽△CBA .(2)、若△ABC的周长为11,请求出AD的长.20. 如图,抛物线与直线相交于点A , B , 点A的横坐标为-4,与轴相交于点C(0,-1).
(1)、求证:△ABD∽△CBA .(2)、若△ABC的周长为11,请求出AD的长.20. 如图,抛物线与直线相交于点A , B , 点A的横坐标为-4,与轴相交于点C(0,-1).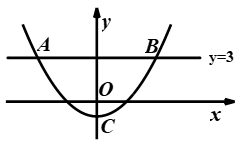 (1)、求出抛物线的解析式.(2)、求出抛物线与x轴的交点坐标.(3)、根据图象,当时,直接写出自变量的取值范围.21. 跳长绳时,当绳甩到最高处时的形状是抛物线,如图正在甩绳的两名同学拿绳的手间距AB为8米,手到地面的距离AO和BD均为0.8米,身高为1.5米的小红站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E , 以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为.
(1)、求出抛物线的解析式.(2)、求出抛物线与x轴的交点坐标.(3)、根据图象,当时,直接写出自变量的取值范围.21. 跳长绳时,当绳甩到最高处时的形状是抛物线,如图正在甩绳的两名同学拿绳的手间距AB为8米,手到地面的距离AO和BD均为0.8米,身高为1.5米的小红站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E , 以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为.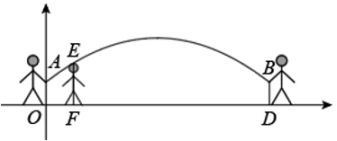 (1)、求该抛物线的解析式.(2)、当绳子甩到最高处时,计算绳子与地面的最大距离.(3)、如果小明站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶正上方0.6米处,求小明的身高.22. 如图1,⊙O的直径AB= , C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D , 连接AD , BD .
(1)、求该抛物线的解析式.(2)、当绳子甩到最高处时,计算绳子与地面的最大距离.(3)、如果小明站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶正上方0.6米处,求小明的身高.22. 如图1,⊙O的直径AB= , C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D , 连接AD , BD .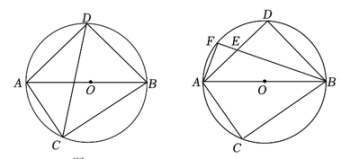 (1)、判断△ABD的形状,并说明理由.(2)、如图2,点F是弧AD上一点,BF交AD于点E.
(1)、判断△ABD的形状,并说明理由.(2)、如图2,点F是弧AD上一点,BF交AD于点E.①求证:FE•EB=AE•DE;
②若AF=0.8,求FE的长.
23. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D , 且AD=8,BD=2,Rt△FEG的直角顶点E在AC边上运动,一条直角边EG经过点B , 且与CD交于点N , 另一条直角边EF与AB交于点M .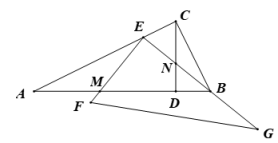 (1)、求证:△AEM∽△CBN;(2)、若E是AC的中点,求的值.(3)、若 , 求的值(用含k的代数式表示).
(1)、求证:△AEM∽△CBN;(2)、若E是AC的中点,求的值.(3)、若 , 求的值(用含k的代数式表示).