青海省西宁市2023年中考数学试卷
试卷更新日期:2023-11-07 类型:中考真卷
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)
-
1. -2023的相反数是( )A、2023 B、-2023 C、 D、2. 算式-3□1的值最小时,□中填入的运算符号是( )A、+ B、- C、× D、÷3. 河湟剪纸被列入青海省第三批省级非物质文化遗产名录,是青海劳动人民结合河湟文化,创造出独具高原特色的剪纸.以下剪纸图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列说法正确的是( )A、检测“神舟十六号”载人飞船零件的质量,应采用抽样调查 B、任意画一个三角形,其外角和是180°是必然事件 C、数据4,9,5,7的中位数是6 D、甲、乙两组数据的方差分别是 , , 则乙组数据比甲组数据稳定5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于P , Q两点,作直线交 , 于点D , E , 连接.下列说法错误的是( )
4. 下列说法正确的是( )A、检测“神舟十六号”载人飞船零件的质量,应采用抽样调查 B、任意画一个三角形,其外角和是180°是必然事件 C、数据4,9,5,7的中位数是6 D、甲、乙两组数据的方差分别是 , , 则乙组数据比甲组数据稳定5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,在中, , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于P , Q两点,作直线交 , 于点D , E , 连接.下列说法错误的是( )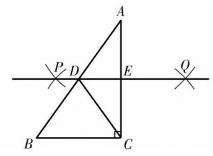 A、直线是的垂直平分线 B、 C、 D、7. 《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,根据题意列方程组得( )A、 B、 C、 D、8. 直线和抛物线(a , b是常数,且)在同一平面直角坐标系中,直线经过点.下列结论:
A、直线是的垂直平分线 B、 C、 D、7. 《孙子算经》中有一道题,原文是:今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,根据题意列方程组得( )A、 B、 C、 D、8. 直线和抛物线(a , b是常数,且)在同一平面直角坐标系中,直线经过点.下列结论:①抛物线的对称轴是直线
②抛物线与x轴一定有两个交点
③关于x的方程有两个根 ,
④若 , 当或时,
其中正确的结论是( )
A、①②③④ B、①②③ C、②③ D、①④二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把最后结果填在答题卡对应的位置上)
-
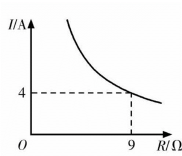
9. 如果气温上升6℃记作+6℃,那么气温下降2℃记作℃.10. 从党的二十大报告中了解到,我国互联网上网人数达1030000000.将1030000000用科学记数法表示为.11. 计算:.12. 有五张看上去无差别的卡片,正面分别写着 , , -0.5, , 0.背面朝上混合后随机抽取一张,取出的卡片正面的数字是无理数的概率是.13. 象征吉祥富贵的丁香花是西宁市市花.为美化丁香大道,园林局准备购买某种规格的丁香花,若每棵6元,总费用不超过5000元,则最多可以购买棵.14. 在中, , , , 则的长约为.(结果精确到0.1.参考数据: , , )15. 已知蓄电池的电压恒定,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,流过的电流是2A,那么此用电器的电阻是Ω.
 16. 在中, , , 点D在边上,连接 , 若为直角三角形,则的度数是.17. 如图,边长为的正方形内接于 , 分别过点A , D作的切线,两条切线交于点P , 则图中阴影部分的面积是.
16. 在中, , , 点D在边上,连接 , 若为直角三角形,则的度数是.17. 如图,边长为的正方形内接于 , 分别过点A , D作的切线,两条切线交于点P , 则图中阴影部分的面积是.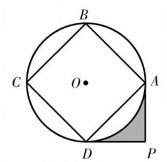 18. 如图,在矩形中,点P在边上,连接 , 将绕点P顺时针旋转90°得到 , 连接..若 , , , 则.
18. 如图,在矩形中,点P在边上,连接 , 将绕点P顺时针旋转90°得到 , 连接..若 , , , 则.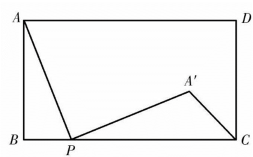
三、解答题(本大题共9小题,第19、20、21、22题每小题7分,第23、24题每小题8分,第25、26题每小题10分,第27题12分,共76分.解答时将文字说明、证明过程或演算步骤写在答题卡相应的位置上)
-
19. 计算:.20. 计算:.21. 先化简,再求值: , 其中a , b是方程的两个根.22. 藏毯作为青海省非物质文化遗产项目之一,与波斯毯、东方毯并称为世界三大名毯.西宁作为藏毯之都,生产的藏毯已成为青海名副其实的特色产品,更是一张通往世界的“金名片”。(1)、为了调查一批藏毯的质量,质检人员从中随机抽取了100件产品进行检测.本次抽样调查的样本容量是;(2)、6月10日是我国文化和自然遗产日.某校举办非遗文化进校园活动,决定从A , B , C , D四名同学中随机抽取两人作为“小小宣传员”,为大家介绍青海藏毯文化.请用画树状图或列表的方法求出A , B两人同时被选中的概率,并列出所有等可能的结果.23. 如图,在中,点E , F分别在 , 的延长线上,且 , 连接与交于点M , 连接 , .
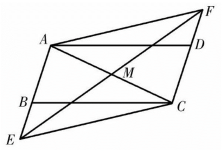 (1)、求证:;(2)、若 , , 求四边形的周长.24. 一次函数的图象与x轴交于点A , 且经过点.
(1)、求证:;(2)、若 , , 求四边形的周长.24. 一次函数的图象与x轴交于点A , 且经过点.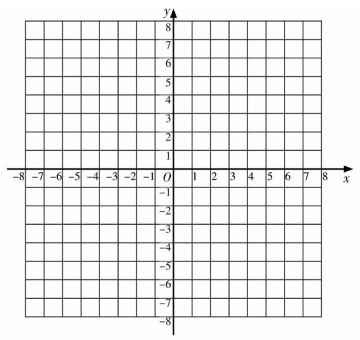 (1)、求点A和点B的坐标;(2)、直接在图6的平面直角坐标系中画出一次函数的图象;(3)、点P在x轴的正半轴上,若是以为腰的等腰三角形,请直接写出所有符合条件的P点坐标.25. 如图,是的弦,半径 , 垂足为D , 弦与交于点F , 连接 , , .
(1)、求点A和点B的坐标;(2)、直接在图6的平面直角坐标系中画出一次函数的图象;(3)、点P在x轴的正半轴上,若是以为腰的等腰三角形,请直接写出所有符合条件的P点坐标.25. 如图,是的弦,半径 , 垂足为D , 弦与交于点F , 连接 , , . (1)、求证:;(2)、若 , , , 求的长.26. 折叠问题是我们常见的数学问题,它是利用图形变化的轴对称性质解决的相关问题.数学活动课上,同学们以“矩形的折叠”为主题开展了数学活动.
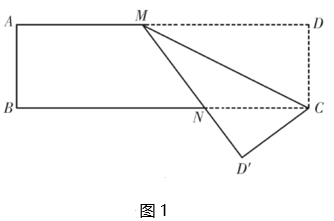
(1)、求证:;(2)、若 , , , 求的长.26. 折叠问题是我们常见的数学问题,它是利用图形变化的轴对称性质解决的相关问题.数学活动课上,同学们以“矩形的折叠”为主题开展了数学活动.【操作】如图1,在矩形中,点M在边上,将矩形纸片沿所在的直线折叠,使点D落在点处,与交于点N.
【猜想】
(1)、【验证】请将下列证明过程补充完整:∵矩形纸片沿所在的直线折叠
∴ ▲
∵四边形是矩形
∴(矩形的对边平行)
∴ ▲ ( )
∴ ▲ ▲ (等量代换)
∴( )
(2)、【应用】如图2,继续将矩形纸片折叠,使恰好落在直线上,点A落在点处,点B落在点处,折痕为.

①猜想与的数量关系,并说明理由;
②若 , , 求的长.
27. 如图,在平面直角坐标系中,直线l与x轴交于点 , 与y轴交于点 , 抛物线经过点A , B , 且对称轴是直线.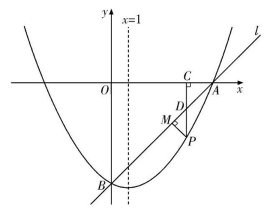 (1)、求直线l的解析式;(2)、求抛物线的解析式;(3)、点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C , 交直线l于点D , 过点P作 , 垂足为M.求的最大值及此时P点的坐标.
(1)、求直线l的解析式;(2)、求抛物线的解析式;(3)、点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C , 交直线l于点D , 过点P作 , 垂足为M.求的最大值及此时P点的坐标.