北京市丰台区2023-2024学年高二上学期期中练习数学试题(A)
试卷更新日期:2023-11-07 类型:期中考试
一、单选题
-
1. 直线的倾斜角为( )A、 B、 C、 D、2. 已知圆 , 则圆心与半径分别为( )A、 , B、 , C、 , D、 ,3. 如图,在平行六面体中,设 , , , 则与向量相等的是( )
 A、 B、 C、 D、4. 已知直线经过点 , 且与直线垂直,则直线的方程为( )A、 B、 C、 D、5. 若直线的方向向量为 , 平面的法向量为 , 则下列选项中能使成立的是( )A、 , B、 , C、 , D、 ,6. 已知直线 , , 若 , 则实数( )A、 B、 C、或 D、或7. 若直线与圆相交于两点,且(其中为原点),则的值为( )A、 B、或 C、 D、或8. 已知圆关于直线对称,则实数( )A、 B、 C、 D、或9. 正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形). 数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体. 如图,已知一个正八面体的棱长为2, , 分别为棱 , 的中点,则直线和夹角的余弦值为( )
A、 B、 C、 D、4. 已知直线经过点 , 且与直线垂直,则直线的方程为( )A、 B、 C、 D、5. 若直线的方向向量为 , 平面的法向量为 , 则下列选项中能使成立的是( )A、 , B、 , C、 , D、 ,6. 已知直线 , , 若 , 则实数( )A、 B、 C、或 D、或7. 若直线与圆相交于两点,且(其中为原点),则的值为( )A、 B、或 C、 D、或8. 已知圆关于直线对称,则实数( )A、 B、 C、 D、或9. 正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形). 数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体. 如图,已知一个正八面体的棱长为2, , 分别为棱 , 的中点,则直线和夹角的余弦值为( ) A、 B、 C、 D、10. 已知圆与圆 , 过动点分别作圆 , 圆的切线 , ( , 分别为切点),若 , 则的最小值为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知圆与圆 , 过动点分别作圆 , 圆的切线 , ( , 分别为切点),若 , 则的最小值为( )A、 B、 C、 D、二、填空题
-
11. 已知直线的斜率为 , 在轴上的截距为 , 则直线的方程为.12. 已知 , , 为空间两两垂直的单位向量,且 , , 则.13. 已知 , , 三点共线,则.14. 已知圆上存在两个点到点的距离均为 , 则实数的一个取值为.15. 已知正方体的棱长为 , 是空间中任意一点.给出下列四个结论:
①若点在线段上运动,则总有;
②若点在线段上运动,则三棱锥体积为定值;
③若点在线段上运动,则直线与平面所成角为定值;
④若点满足 , 则过点 , , 三点的正方体截面面积的取值范围为.
其中所有正确结论的序号为.
三、问答题
-
16. 已知圆.(1)、求经过点的圆的切线方程;(2)、求直线被圆截得的弦长.17. 如图,在直三棱柱中, , , , 分别是 , 的中点.
 (1)、求证:平面;(2)、求直线与平面所成角的正弦值.18. 如图,在四棱锥中,底面为平行四边形, , , , , , 为棱的中点.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值.18. 如图,在四棱锥中,底面为平行四边形, , , , , , 为棱的中点.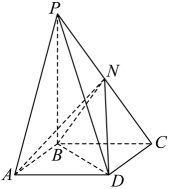
条件①:;
条件②:平面平面.
从条件①和条件②这两个条件中选择一个作为已知,完成下列问题:
(1)、求证:;(2)、若点在线段上,且点到平面的距离为 , 求线段的长.注:如果选择条件①和条件②分别解答,按第一个解答计分.
19. 在平面直角坐标系中,已知圆的圆心在直线上,且半径为.(1)、若圆心也在直线上,求圆的方程;(2)、已知点 , 若圆上存在点 , 使 , 求圆心的横坐标的取值范围.
