北京市丰台区2023-2024学年高二上学期期中练习数学试题（B）

试卷更新日期：2023-11-07 类型：期中考试

进入出卷网下载

一、单选题

1. 直线 $y = \sqrt{3} x$ 的倾斜角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
2. 已知向量 $\vec{a} = (2 ， - 1 ， 3)$ ， $\vec{b} = (4 ， x ， y)$ ，且 $\vec{a} / / \vec{b}$ ，则 $x + y =$ （）

A、 $- 4$ B、 $- 2$ C、 $4$ D、 $2$

查看试题解析
3. 已知点 $B$ 是点 $A (2 ， - 3 ， 4)$ 在坐标平面 $O x y$ 内的射影，则点 $B$ 的坐标为（）

A、 $(2 ， - 3 ， 0)$ B、 $(2 ， 0 ， 4)$ C、 $(0 ， - 3 ， 4)$ D、 $(2 ， 3 ， 4)$

查看试题解析
4. 已知直线 $l$ 经过点 $A (- 3 ， 2)$ ，且与直线 $x + 2 y - 2 = 0$ 垂直，则直线 $l$ 的方程为（）

A、 $x + 2 y - 1 = 0$ B、 $x - 2 y + 7 = 0$ C、 $2 x + y + 4 = 0$ D、 $2 x - y + 8 = 0$

查看试题解析
5. 圆 $x^{2} + {(y - 1)}^{2} = 4$ 截 $x$ 轴所得弦的长度为（）

A、 $2$ B、 $2 \sqrt{3}$ C、 $2 \sqrt{5}$ D、 $4$

查看试题解析
6. 若直线 $2 x - y + m = 0$ 和直线 $3 x - y + 3 = 0$ 的交点在第二象限，则 $m$ 的取值范围为（）

A、 $(- \infty ， 3)$ B、 $(2 ， + \infty)$ C、 $(- \infty ， 2) \cup (3 ， + \infty)$ D、 $(2 ， 3)$

查看试题解析
7. 如图，在平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，若 $\vec{D_{1} M} = x \vec{A B} + y \vec{A D} + z \vec{A A_{1}}$ ，则有序实数组 $(x ， y ， z) =$ （）

A、 $(- \frac{1}{2} ， \frac{1}{2} ， 1)$ B、 $(\frac{1}{2} ， \frac{1}{2} ， 1)$ C、 $(\frac{1}{2} ， - \frac{1}{2} ， - 1)$ D、 $(- \frac{1}{2} ， - \frac{1}{2} ， - 1)$

查看试题解析
8. 已知直线 $l_{1}$ ： $a x - 3 y + 12 = 0$ ， $l_{2}$ ： $x + (a - 4) y + 4 = 0$ ，若 $l_{1} ∥ l_{2}$ ，则实数 $a =$ （）

A、 $1$ B、 $3$ C、 $1$ 或 $0$ D、 $1$ 或 $3$

查看试题解析
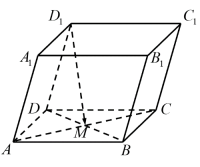9. 已知平面 $α = {P | \vec{n} \cdot \vec{A P} = 0}$ ，其中点 $A (1 ， 1 ， 2)$ ，向量 $\vec{n} = (1 ， 1 ， 1)$ ，则下列各点中在平面 $α$ 内的是（）

A、 $(2 ， - 1 ， - 1)$ B、 $(0 ， 3 ， 1)$ C、 $(- 2 ， 4 ， 3)$ D、 $(5 ， - 1 ， - 2)$

查看试题解析
10. 正多面体也称柏拉图立体，被誉为最有规律的立体结构，是所有面都只由一种正多边形构成的多面体（各面都是全等的正多边形）. 数学家已经证明世界上只存在五种柏拉图立体，即正四面体、正六面体、正八面体、正十二面体、正二十面体. 如图，已知一个正八面体 $A B C D E F$ 的棱长为2， $M$ ， $N$ 分别为棱 $A D$ ， $A C$ 的中点，则直线 $B N$ 和 $F M$ 夹角的余弦值为（）

A、 $\frac{5}{6}$ B、 $\frac{\sqrt{11}}{6}$ C、 $\frac{\sqrt{21}}{6}$ D、 $\frac{\sqrt{15}}{6}$

查看试题解析

二、填空题

11. 以 $A (2 ， - 1)$ 为圆心，半径为2的圆的标准方程为.

查看试题解析
12. 已知点 $A (1 ， 0 ， 2)$ ， $B (1 ， 2 ， 5)$ ， $C (- 2 ， 3 ， 6)$ ，则 $\overset{\overset{}{\to}}{A B} - \overset{\overset{}{\to}}{A C} =$ .

查看试题解析
13. 已知直线 $l$ 经过点 $A (1 ， 4)$ ，且斜率为 $2$ ，则直线 $l$ 的一个方向向量为.

查看试题解析
14. 已知点 $P$ 为圆 $x^{2} + y^{2} = 1$ 上一点，记 $d$ 为点 $P$ 到直线 $x - m y - 2 = 0$ 的距离.当 $m$ 变化时， $d$ 的最大值为.

查看试题解析
15. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $A D = D D_{1} = 1$ ，点 $E$ 是棱 $C D$ 上的动点，给出下列4个结论：
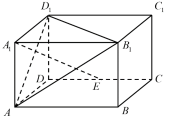
① $\vec{A B} + \vec{A A_{1}} - \vec{A D_{1}} = \vec{B_{1} D_{1}}$ ；
② $A D_{1} ⊥ A_{1} E$ ；
③若 $E$ 为 $C D$ 中点，则点 $B_{1}$ 到直线 $A_{1} E$ 的距离为 $\frac{2 \sqrt{2}}{3}$ ；
④存在点 $E$ ，使得 $A_{1} E ⊥$ 平面 $A B_{1} D_{1}$ ．
其中所有正确结论的序号是.

查看试题解析

三、问答题

16. 在 $△ A B C$ 中， $A (- 3 ， 0)$ ， $B (1 ， 4)$ ， $C (3 ， - 3)$ .

(1)、求边 $A B$ 所在直线的方程；

(2)、求边 $A B$ 上的中线所在直线的方程.

查看试题解析
17. 已知向量 $\vec{a} = (1 ， 3 ， 2)$ ， $\vec{b} = (- 2 ， 1 ， 4)$ ， $\vec{c} = (5 ， 1 ， x)$ .

(1)、若 $\vec{a} ⊥ \vec{c}$ ，求实数 $x$ 的值；

(2)、求 $| 2 \vec{a} - \vec{b} |$ ；

(3)、若 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 不能构成空间向量的一个基底，求实数 $x$ 的值.

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是正方形， $P D ⊥$ $A D$ ， $P D = 2 D C = 4$ ， $E$ 是棱 $P A$ 的中点.

(1)、求证： $P C$ //平面 $B D E$ ；

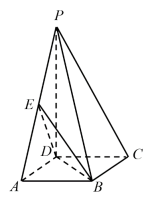(2)、再从条件①、条件②这两个条件中选择一个作为已知，求平面 $B D E$ 与平面 $A B C D$ 夹角的余弦值.
条件①：平面 $P A D ⊥$ 平面 $A B C D$ ；
条件②： $P D ⊥ D C$ .
注：如果选择条件①和条件②分别解答，按第一个解答计分.

查看试题解析
19. 已知圆 $M_{1}$ ： $x^{2} + 2 x + y^{2} - 8 = 0$ .

(1)、求圆 $M_{1}$ 的圆心坐标以及半径；

(2)、求经过点 $P_{0} (2 ， 1)$ 的圆 $M_{1}$ 的切线方程；

(3)、若圆 $M_{1}$ 与圆 $M_{2}$ ： $(x - 2)^{2} + (y - 4)^{2} = m$ $(m > 0)$ 有公共点，求实数 $m$ 的取值范围.

查看试题解析
20. 赵州桥，又名安济桥，位于河北省石家庄市赵县的洨河上，距今已有 $1400$ 多年的历史，是保存最完整的古代单孔敞肩石拱桥，其高超的技术水平和不朽的艺术价值，彰显了中国劳动人民的智慧和力量.2023年以来，中国文旅市场迎来强劲复苏，某地一旅游景点为吸引游客，参照赵州桥的样式在景区兴建圆拱桥，该圆拱桥的圆拱跨度为 $16 m$ ，拱高为 $4 m$ ，在该圆拱桥的示意图中建立如图所示的平面直角坐标系．

(1)、求这座圆拱桥的拱圆的方程；

(2)、若该景区游船宽 $10 m$ ，水面以上高 $3 m$ ，试判断该景区游船能否从桥下通过，并说明理由. $(\sqrt{3} \approx 1.732)$

查看试题解析
21. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ B A C = 90 °$ ， $A B = A C = 2$ ， $A A_{1} = 3$ ． $M$ ， $N$ 分别为棱 $A B$ ， $B_{1} C_{1}$ 的中点， $B C_{1}$ 与 $B_{1} C$ 交于点 $P$ ．

(1)、求直线 $A A_{1}$ 与平面 $A_{1} C M$ 所成角的正弦值；

(2)、求直线 $B C_{1}$ 到平面 $A_{1} C M$ 的距离；

(3)、在线段 $A_{1} N$ 上是否存在点 $Q$ ，使得 $P Q / /$ 平面 $A_{1} C M$ ？若存在，求 $\frac{A_{1} Q}{A_{1} N}$ 的值；若不存在，请说明理由.

查看试题解析