江苏省苏州市2023-2024学年高一上学期11月期中摸底数学试题
试卷更新日期:2023-11-07 类型:期中考试
一、单选题
-
1. 已知全集 , , 则集合( )A、 B、 C、 D、2. 函数的定义域是( )A、 B、 C、 D、3. “函数在上为减函数”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件4. 函数 的图象大致为( )A、
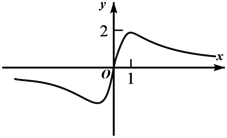 B、
B、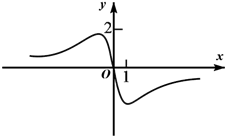 C、
C、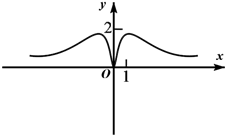 D、
D、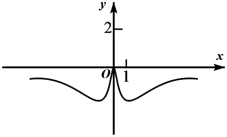 5. 设函数 , 若 , 则( )A、1 B、2 C、 D、6. 专家对某地区新冠肺炎爆发趋势进行研究发现,从确诊第一名患者开始累计时间 (单位:天)与病情爆发系数 之间,满足函数模型: ,当 时,标志着疫情将要大面积爆发,则此时 约为( )
5. 设函数 , 若 , 则( )A、1 B、2 C、 D、6. 专家对某地区新冠肺炎爆发趋势进行研究发现,从确诊第一名患者开始累计时间 (单位:天)与病情爆发系数 之间,满足函数模型: ,当 时,标志着疫情将要大面积爆发,则此时 约为( )(参考数据: )
A、38 B、40 C、45 D、477. 函数在 上单调递增,且 , 则实数的取值范围是A、 B、 C、 D、8. 黎曼函数是由德国数学家黎曼发现并提出的,在高等数学中有着广泛的应用,在上的定义为:当( , 且 , 为互质的正整数)时,;当或或为内的无理数时,.已知 , , , 则( )注: , 为互质的正整数 , 即为已约分的最简真分数.A、的值域为 B、 C、 D、以上选项都不对二、多选题
-
9. 图中阴影部分用集合表示正确的是( )
 A、 B、 C、 D、10. 下列命题中假命题有( )A、 , B、“且”是“”的充要条件 C、 , D、函数的值域为11. 若 , ,则( )A、 B、 C、 D、12. 下列说法正确的是( )A、若为正数,且满足 , 则的最小值为 B、已知实数 , 则表达式的最小值为 C、已知实数且 , 满足 , 则的最小值为 D、若两个不相等的正数满足 , 则的最小值为
A、 B、 C、 D、10. 下列命题中假命题有( )A、 , B、“且”是“”的充要条件 C、 , D、函数的值域为11. 若 , ,则( )A、 B、 C、 D、12. 下列说法正确的是( )A、若为正数,且满足 , 则的最小值为 B、已知实数 , 则表达式的最小值为 C、已知实数且 , 满足 , 则的最小值为 D、若两个不相等的正数满足 , 则的最小值为三、填空题
-
13. 命题“ ”的否定是.14. 已知幂函数的图象经过点 , 则该函数的单调区间为.15. 已知偶函数在区间上单调递减,且 , 则不等式的解集为.16. 已知函数 , , 为常数,若对于任意 , ,且 ,都有 则实数 的取值范围为.
四、解答题
-
17.(1)、求的值;(2)、已知 , 求的值.18. 已知命题:“ , 都有不等式成立”是真命题.(1)、求实数的取值集合;(2)、设不等式的解集为 , 若是的充分条件,求实数的取值范围.19. 已知函数是定义在上的奇函数,且.(1)、求的值;(2)、用单调性定义证明:函数在区间上单调递增;(3)、若 , 求实数的取值范围.20. 某公司每月最多生产100台报警系统装置,生产台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.(1)、求利润函数及利润函数的最大值;(2)、为了促销,如果每月还需投入500元的宣传费用,设每台产品的利润为 , 求的最大值及此时的值.