（人教版）2023-2024学年八年级数学上册 14.3 因式分解同步分层训练（培优卷）

试卷更新日期：2023-11-07 类型：同步测试

进入出卷网下载

一、选择题

1. 已知二次三项式 $x^{2} - kx - 15$ 能分解成系数为整数的两个一次因式的积，则整数 $k$ 的取值范围有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若 $4 x^{2} + 5 x + k$ 有一个因式为 $(x - 3)$ ，则k的值为（）

A、17 B、51 C、－51 D、－57

查看试题解析
3. 如果二次三项式 $x^{2} - a x - 9$ （ $a$ 为整数）在整数范围内可以分解因式，那么 $a$ 可取值的个数是（）

A、2个 B、3个 C、4个 D、无数个

查看试题解析
4. 因式分解x²+mx﹣12＝（x+p）（x+q），其中m、p、q都为整数，则这样的m的最大值是（）

A、1 B、4 C、11 D、12

查看试题解析
5. 已知甲、乙、丙均为x的一次多项式，且其一次项的系数皆为正整数．若甲与乙相乘为x²－4，乙与丙相乘为x²＋15x－34，则甲与丙相加的结果为（）

A、2x＋19 B、2x－19 C、2x＋15 D、2x－15

查看试题解析
6. 下列二次三项式在实数范围内不能因式分解的是（）

A、 $6 x^{2} + x - 15$ B、 $3 y^{2} + 7 y + 3$ C、 $x^{2} - 2 x - 4$ D、 $2 x^{2} - 4 x y + 5 y^{2}$

查看试题解析
7. 已知多项式 2x³-x²＋m 分解因式后有一个因式是 x＋1，则 m 的值为（）

A、－3 B、3 C、1 D、-1

查看试题解析
8. 若 $a - b = 8$ ， $a^{2} - b^{2} = 72$ ，则 $a + b$ 的值为（）

A、 $9$ B、 $- 9$ C、 $27$ D、 $- 27$

查看试题解析
9. 已知： $a + b = 5 ， a - b = 1$ ，则 $a^{2} - b^{2} =$ （）

A、5 B、4 C、3 D、2

查看试题解析
10. 已知 $d = x^{4} - 2 x^{3} + x^{2} - 12 x - 5$ ，则当 $x^{2} - 2 x - 5 = 0$ ， $d$ 的值为（）

A、25 B、20 C、15 D、10

查看试题解析

二、填空题

11. 因式分解： $a^{2} (x - y) + (y - x) =$ ．

查看试题解析
12. 分解因式： $3 m^{3} - 12 m =$ ．

查看试题解析
13. 已知 $a - b = 1$ ， $a b = 2$ 则 $a^{2} b - a b^{2}$ 的值为.

查看试题解析
14. 在实数范围内分解因式： $3 x^{2} - x - 1 =$ ．

查看试题解析
15. 已知 $a^{2} - b^{2} = 8$ ， $a - b = 4$ ，则 $a + b =$ .

查看试题解析

三、解答题

16. 已知，长方形的周长为30cm，两相邻的边长为xcm，ycm，且x³+x²y-4xy²-4y³=0，求长方形的对角线长和面积．

查看试题解析
17. 已知a、b、c是△ABC的三边长，且a²+2b²+c²﹣2b（a+c）=0，试判断△ABC的形状，并证明你的结论．

查看试题解析
18. 请认真观察图形，解答下列问题：

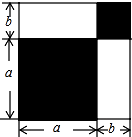(1)、根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；

(2)、由（1），你能得到怎样的等量关系？请用等式表示；

(3)、如果图中的a，b（a＞b）满足a²＋b²＝53，ab＝14，求：①a＋b的值；②a⁴－b⁴的值．

查看试题解析
19. 常用的分解因式的方法有提取公因式法、公式法及十字相乘法，但有更多的多项式只用上述方法就无法分解，如x²－4y²－2x＋4y，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了．过程为：x²－4y²－2x＋4y＝(x＋2y)(x－2y)－2(x－2y)＝(x－2y)(x＋2y－2)．
这种分解因式的方法叫分组分解法．利用这种方法解决下列问题：

(1)、分解因式x²－2xy＋y²－16；

(2)、△ABC三边a，b，c 满足a²－ab－ac＋bc＝0，判断△ABC的形状．

查看试题解析

四、综合题

20. 定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“湘一数”.将一个“湘一数”的个位数字与十位数字对调后得到一个新的两位数，把这个两位数与原两位数的和与11的商记为 $f (a)$ .例如：a=23，对调个位数字与十位数字得到新两位数32，新两位数与原两位数的和为23+32=55，和与11的商为55÷11=5，所以 $f (23) = 5$ .
根据以上定义，回答下列问题：

(1)、填空：①下列两位数：50、42，33中，“湘一数”为；②计算： $f (45) =$ .

(2)、如果一个“湘一数”b的十位数字是k，个位数字是 $2 (k + 1)$ ，且 $f (b) = 8$ ，请求出“湘一数”b；

(3)、如果一个“湘一数”c，满足 $c - 5 f (c) > 30$ ，求满足条件的c的值.

查看试题解析
21. 如图

我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图（1）可以用来解释 $a^{2} + 2 a b + b^{2} = {(a + b)}^{2}$ ，实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解．

如图（2），将一张长方形纸板按图中虚线裁剪成九块，其中有两块是边长都为 $m$ 的大正方形，两块是边长都为 $n$ 的小正方形，五块是长为 $m$ ，宽为 $n$ 的全等小长方形，且 $m > n$ ．（以上长度单位： $c m$ ）

(1)、观察图形，可以发现代数式 $2 m^{2} + 5 m n + 2 n^{2}$ 可以分解因式为

(2)、若每块小长方形的面积为 $10 c m^{2}$ ，四个正方形的面积和为 $58 c m^{2} ，$ 试求图中所有裁剪线（虚线部分）长之和．

查看试题解析
22. 综合与实践
下面是某同学对多项式 $(x^{2} - 4 x) (x^{2} - 4 x + 8) + 16$ 进行因式分解的过程：

解：设 $x^{2} - 4 x = y$ ，

原式 $= y (y + 8) + 16$ （第一步）

$= y^{2} + 8 y + 16$ （第二步）

$= {(y + 4)}^{2}$ （第三步）

$= {(x^{2} - 4 x + 4)}^{2}$ （第四步）．

回答下列问题：

(1)、该同学第二步到第三步运用了________．

A、提取公因式 B、平方差公式 C、两数差的完全平方公式 D、两数和的完全平方公式

(2)、该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”），若不彻底，则该因式分解的最终结果为．

(3)、请你模仿上述方法，对多项式 $(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4$ 进行因式分解．

查看试题解析
23. 阅读下列文字与例题，并解答。
将一个多项式分组进行因式分解后，可用提公因式法或公式法继续分解的方法称作分组分解法。例如：以下式子的分解因式的方法叉称为分组分解法。

$a^{2} + 2 a b + b^{2} + a c + b c = (a^{2} + 2 a b + b^{2}) + (a c + b c) = {(a + b)}^{2} + c (a + b) = (a + b) (a + b + c)$

(1)、试用“分组分解法”分解因式： $x^{2} - y^{2} + x z - y z$

(2)、已知四个实数a，b，c，d满足 $a \neq b ， c \neq d$ 。并且 $a^{2} + a c = 12 k$ ， $b^{2} + b c = 12 k$ ， $c^{2} + a c = 24 k$ ， $d^{2} + a d = 24 k$ 同时成立。
①当k=1时，求a+c的值；

②当k≠0时，用含a的代数式分别表示b、c、d。

查看试题解析

（人教版）2023-2024学年八年级数学上册 14.3 因式分解 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 14.3 因式分解同步分层训练（培优卷）