湖南省邵阳市邵东市2023-2024学年九年级上学期月考数学试题
试卷更新日期:2023-11-06 类型:月考试卷
一、选择题(每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.)
-
1. 已知函数的图象过点 , 则该函数的图象经过( )A、第二、四象限 B、第二、三象限 C、第一、三象限 D、第三、四象限2. 一元二次方程配方后化为( )A、 B、 C、 D、3. 把写成比例式,其中错误的是( )A、 B、 C、 D、4. 已知点、是反比例函数图象上的两点,若 , 则有( )A、 B、 C、 D、5. 若是关于x的方程的一个根,则的值是( )A、-3 B、-1 C、3 D、16. 点B是线段AC的黄金分割点,且ABBC.若AC=4,则BC的长为( )A、 B、 C、 D、7. 如图所示,利用围墙的一边用13m的铁丝网围成一个面积为的矩形,求这个矩形中与围墙平行的一边长度,如果设平行于围墙的一边为 , 那么可得方程( )
 A、 B、 C、 D、8. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( )
A、 B、 C、 D、8. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( ) A、 B、 C、 D、9. 已知关于x的一元二次方程有实根,则m的取值范围是( )A、 B、且 C、 D、且10. 函数和在同一坐标系中的图象可以大致是( )A、
A、 B、 C、 D、9. 已知关于x的一元二次方程有实根,则m的取值范围是( )A、 B、且 C、 D、且10. 函数和在同一坐标系中的图象可以大致是( )A、 B、
B、 C、
C、 D、
D、
二、填空题(每小题3分,共24分)
-
11. 已知点与点在反比例函数的图像上,则m的值为.12. 一元二次方程的根是.13. 若 , 则的值为.14. 如图,已知直线 , 直线m、n分别与直线、、分别交于点A、B、C、D、E、F,若 , , 则的值为.
 15. 已知关于x的方程 , 若该方程的一个根是-1,则另一个根是.16. 如图,在中,D是AB边上的一点,连接CD,请添加一个适当的条件 , 使.(只填一个即可)
15. 已知关于x的方程 , 若该方程的一个根是-1,则另一个根是.16. 如图,在中,D是AB边上的一点,连接CD,请添加一个适当的条件 , 使.(只填一个即可) 17. 如图,在中,的平分线BF分别与AC、AD交于点E、F.若 , , 则的值是.
17. 如图,在中,的平分线BF分别与AC、AD交于点E、F.若 , , 则的值是.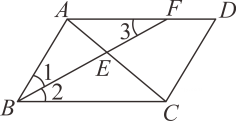 18. 如图,是直角三角形, , , 点A在反比例函数的图像上,若点B在反比例函数的图像上,则.
18. 如图,是直角三角形, , , 点A在反比例函数的图像上,若点B在反比例函数的图像上,则.
三、解方程(共8分)
-
19.(1)、(2)、
四、解答题(第20-25题,每题8分,第26题10分,共58分)
-
20. 已知是关于x的反比例函数.(1)、若时,y随x的增大而减小,求m的值;(2)、若该反比例函数图象经过第二象限内点 , 求n的值.21. 在正方形ABCD中,E是边AD的中点,连接BE,过点E作 , 分别交CD及BC边延长线于点F,G.
 (1)、求证:;(2)、若正方形的边长为4,求BG的长.22. 某商场销售一批衬衫,平均每天可销售出20件,每件盈利50元,为扩大销售盈利,商场决定采取适当的降价措施,但要求每件盈利不少于30元,经调查发现,若每件衬衫每降价1元,则商场每天可多销售2件.(1)、若每件衬衫降价5元,则每天可盈利多少元?(2)、若商场平均每天盈利1600元,则每件衬衫应降价多少元?23. 已知 , 点E是BA延长线上一点,CE与AD,BD分别相交于点G,F.求证:.
(1)、求证:;(2)、若正方形的边长为4,求BG的长.22. 某商场销售一批衬衫,平均每天可销售出20件,每件盈利50元,为扩大销售盈利,商场决定采取适当的降价措施,但要求每件盈利不少于30元,经调查发现,若每件衬衫每降价1元,则商场每天可多销售2件.(1)、若每件衬衫降价5元,则每天可盈利多少元?(2)、若商场平均每天盈利1600元,则每件衬衫应降价多少元?23. 已知 , 点E是BA延长线上一点,CE与AD,BD分别相交于点G,F.求证:.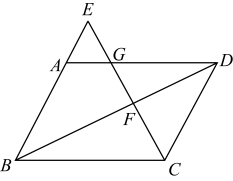 24. 已知关于x的一元二次方程有两实数根.(1)、求m的取值范围;(2)、若 , 是该方程的两个根,且 , 求m的值.
24. 已知关于x的一元二次方程有两实数根.(1)、求m的取值范围;(2)、若 , 是该方程的两个根,且 , 求m的值.
-

