（人教版）2023-2024学年八年级数学上册 14.2 乘法公式同步分层训练（培优卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为40；其中5个如图2摆放，构造出一个长方形，其中阴影部分面积为100（各个小长方形之间不重叠不留空），则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析
2. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）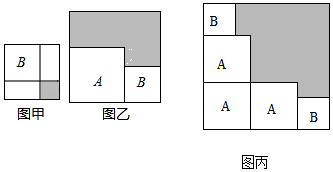

A、28 B、29 C、30 D、31

查看试题解析
3. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{1010} + 1)$ 化简的结果为（）

A、 $2^{1010} - 1$ B、 $2^{1010} + 1$ C、 $2^{2020} - 1$ D、 $2^{2020} + 1$

查看试题解析
4. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1)$ 的计算结果的个位数字是（）

A、8 B、6 C、2 D、0

查看试题解析
5. 若 $a^{4} + b^{4} + a^{2} b^{2} = 5$ ， $a b = 2$ ，则 $a^{2} + b^{2}$ 的值是（）

A、－2 B、2 C、3 D、±3

查看试题解析
6. 若 $a - b = 3$ , $a^{2} + b^{2} = 5$ ,则ab的值为（）

A、1 B、-1 C、2 D、-2．

查看试题解析
7. 计算(2+1)(2²+1)(2⁴+1)(2⁸+1)+1的值是（）

A、1024 B、2⁸+1 C、2¹⁶+1 D、2¹⁶

查看试题解析
8. 已知 $x + \frac{1}{x} = 3$ ，则下列三个等式：① $x^{2} + \frac{1}{x^{2}} = 7$ ，② $x - \frac{1}{x} = \sqrt{5}$ ，③ $2 x^{2} - 6 x = - 2$ 中，正确的个数有（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
9. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形，如图所示，如果大正方形的面积是100，小正方形的面积为20，那么每个直角三角形的周长为（）

A、10+6 $\sqrt{5}$ B、10+10 $\sqrt{2}$ C、10+4 $\sqrt{10}$ D、24

查看试题解析
10. 已知a+ $\frac{1}{a}$ =3，则a²+ $\frac{1}{a^{2}}$ 的值是（）

A、9 B、7 C、5 D、3

查看试题解析

二、填空题

11. $(1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) + 1$ 的结果是．

查看试题解析
12. 计算：（2+1）（2²+1）（2⁴+1）…（2³²+1）+1＝．

查看试题解析
13. 计算：（2+1）（2²+1）（2⁴+1）（2⁸+1）（2¹⁶+1）=（结果可用幂的形式表示）

查看试题解析
14. 已知 $a$ ， $b$ ， $c$ 为 $Δ A B C$ 的三边长，且 $a^{2} + b^{2} = 8 a + 12 b - 52$ ，其中 $c$ 是 $Δ A B C$ 中最短的边长，且 $c$ 为整数，则 $c =$ ．

查看试题解析
15. 将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为.

查看试题解析

三、解答题

16. 如图1是一个长为4a ，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图2的正方形．

(1)、由图2可以直接写出（a+b）² ，（a-b）² ， ab之间的一个等量关系是；

(2)、根据（1）中的结论，解决下列问题：3x+4y＝10，xy＝2，求3x-4y的值；

(3)、两个正方形ABCD ， AEFG如图3摆放，边长分别为x ， y ．若x²+y²＝58，BE＝4，求图中阴影部分面积和．

查看试题解析
17. 已知a﹦ $\frac{1}{2}$ （ $\sqrt{5}$ + $\sqrt{3}$ ），b﹦ $\frac{1}{2}$ （ $\sqrt{5}$ ﹣ $\sqrt{3}$ ），求a²﹣ab+b²的值．

查看试题解析
18. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如
图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，请求出其阴影部分的面积为多少．

查看试题解析
19. 为创建文明校园环境，高校长制作了“节约用水”“讲文明，讲卫生”等宣传标语，标语由如图 $①$ 所示的板材裁剪而成，其为一个长为 $2 m$ ，宽为 $2 n$ 的长方形板材，将长方形板材沿图中虚线剪成四个形状和大小完全相同的小长方形标语，在粘贴过程中，同学们发现标语可以拼成图 $②$ 所示的一个大正方形．

(1)、用两种不同方法表示图 $②$ 中小正方形 $($ 阴影部分 $)$ 面积：
方法一： $S_{小正方形} =$ ；
方法二： $S_{小正方形} =$ ；

(2)、 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $4 m n$ 这三个代数式之间的等量关系为；

(3)、根据 $(2)$ 题中的等量关系，解决如下问题：
$①$ 已知： $a - b = 5$ ， $a b = - 6$ ，求： $(a + b)^{2}$ 的值；
$②$ 已知： $a - \frac{1}{a} = 1$ ，求： $(a + \frac{1}{a})^{2}$ 的值．

查看试题解析

四、综合题

20. 我们将 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 进行变形，如： $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b$ ， $a b = \frac{{(a + b)}^{2} - (a^{2} + b^{2})}{2}$ 等.根据以上变形解决下列问题：

(1)、已知 $a^{2} + b^{2} = 12$ ， ${(a + b)}^{2} = 20$ ，则 $a b =$ ；

(2)、若x满足 ${(2022 - x)}^{2} + {(x - 2019)}^{2} = 2020$ ，求 $(2022 - x) (x - 2019)$ 的值；

(3)、如图，在长方形 $A B C D$ 中， $A B = 10$ ， $B C = 6$ ，点E、F分别是 $B C$ 、 $C D$ 上的点，且 $B E = D F = x$ ，分别以 $F C$ 、 $C E$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，若长方形 $C E P F$ 的面积为40，求图中阴影部分的面积和.

查看试题解析
21. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为 $a$ 的正方形， $B$ 种纸片是边长为 $b$ 的正方形， $C$ 种纸片是长为 $b$ ，宽为 $a$ 的长方形.并用A种纸片一张， $B$ 种纸片一张， $C$ 种纸片两张拼成如图2的大正方形.

(1)、请用两种不同的方法表示图2中大正方形的面积并用等号连接：

(2)、根据（1）题中的等量关系，解决如下问题：
①已知： $a + b = 5$ ， ${(a - b)}^{2} = 13$ ，求 $a b$ 的值；
②已知 ${(a - 2022)}^{2} + {(a - 2021)}^{2} = 5$ ，求 $(2022 - a) (a - 2021)$ 的值.

查看试题解析
22. 综合与探究
【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如，由图可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，基于此，请解答下列问题．

(1)、【直接应用】若 $x + y = 3$ ， $x^{2} + y^{2} = 5$ ，求 $x y$ 的值．

(2)、【类比应用】若 $x (3 - x) = 2$ ，则 $x^{2} + {(3 - x)}^{2} =$ ．

(3)、【知识迁移】将两块全等的特制直角三角板（ $∠ A O B = ∠ C O D = 90 °$ ）按如图所示的方式放置，其中点 $A$ ， $O$ ， $D$ 在同一直线上，点 $B$ ， $O$ ， $C$ 也在同一直线上，连接 $A C$ ， $B D$ ．若 $A D = 14$ ， $S_{△ A O C} + S_{△ B O D} = 50$ ，求一块直角三角板的面积．

查看试题解析
23. 乘法公式的探究及应用．

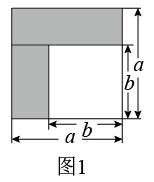
(1)、如图1，若将阴影部分裁剪下来，重新拼成一个矩形，如图2，通过比较图1、图2阴影部分的面积，可以得到整式乘法公式：；

(2)、2¹⁶-1可以被10和20之间某两个整数整除，则这两个数分别为．

(3)、计算： $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) + 1$ ．

查看试题解析

（人教版）2023-2024学年八年级数学上册 14.2 乘法公式 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 14.2 乘法公式同步分层训练（培优卷）