（人教版）2023-2024学年八年级数学上册 14.2 乘法公式同步分层训练（提升卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $a - \frac{1}{a} = 3$ ，则 $(a + \frac{1}{a})^{2}$ 的值是（）

A、 $5$ B、 $6$ C、 $12$ D、 $13$

查看试题解析
2. 用如图所示的几何图形的面积可以解释的代数恒等式是（）

A、 $(2 a)^{2} = 4 a^{2}$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $2 a (a + b) = 2 a^{2} + 2 a b$ D、 $2 a (2 a + b) = 4 a^{2} + 2 a b$

查看试题解析
3. 下列从左到右的变式正确的是（）

A、-a+b+c=-（a+b-c） B、-（a-b+c）=-a+b-c C、a-b+c=-（a+b-c） D、-（a-b+c）=-a-b-c

查看试题解析
4. 下列计算正确的是（　　）

A、a²+a⁴＝a⁶ B、 ${(\frac{a}{b})}^{4} = \frac{a^{4}}{b^{4}}$ C、（-a²）³＝a⁶ D、（a-b）（b+a）＝b²-a²

查看试题解析
5. 已知 $a$ 、 $b$ 、 $c$ 为 $△ A B C$ 的三边长，且 $a^{2} + a c = b^{2} + b c$ ，则 $△ A B C$ 是（）

A、等腰直角三角形 B、直角三角形 C、等边三角形 D、等腰三角形

查看试题解析
6. 已知实数 $a$ ， $b$ ， $c$ 满足 $a - 3 b + c = 0$ ， $a + 3 b + c < 0$ ，则下列选项中正确的（）

A、 $b < 0$ ， $b^{2} - \frac{4}{9} a c \leq 0$ B、 $b < 0$ ， $b^{2} - \frac{4}{9} a c \geq 0$ C、 $b > 0$ ， $b^{2} - \frac{4}{9} a c \leq 0$ D、 $b > 0$ ， $b^{2} - \frac{4}{9} a c \geq 0$

查看试题解析
7. 已知 $\frac{1}{4} m^{2} + \frac{1}{4} n^{2} = n - m - 2$ ，则 $\frac{1}{m} - \frac{1}{n}$ 的值等于（）

A、1 B、0 C、 $- 1$ D、 $- \frac{1}{4}$

查看试题解析
8. 下列计算正确的是（）

A、 $(- 2 a)^{3} = - 6 a^{3}$ B、 $4 a^{3} \cdot 3 a^{2} = 12 a^{5}$
C、 $- 8 a^{4} \div 4 a = - 2 a$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
9. 下列计算正确的是（）

A、 $x^{0} = 1$ B、 $(x + y)^{2} = x^{2} + y^{2}$
C、 $x^{6} \div x^{2} = x^{4}$ D、 $x^{2} \cdot x^{3} = x^{6}$

查看试题解析
10. 下列运算正确的是（）

A、 $a + a^{2} = a^{3}$ B、 ${(- 2 x + y)}^{2} = 4 x^{2} - 4 x y + y^{2}$ C、 $- a (b - c) = - a b - a c$ D、 $3 x y^{2} \div 3 x^{2} y = 1$

查看试题解析

二、填空题

11. 计算： $2015 \times 2017 - 201 6^{2} =$ ．

查看试题解析
12. 已知 $x^{2} - y^{2} = 8$ ，且 $x + y = 4$ ，则 $x - y =$ ．

查看试题解析
13. 已知 $x + y = 4$ ， $x - y = 9$ ，则 $x^{2} - y^{2} =$ ．

查看试题解析
14. 分解因式 $- 9 - a^{2} + 6 a =$ ．

查看试题解析
15. x²-2x+y=x²-()．

查看试题解析

三、解答题

16. “筑牢民生之基，增强百姓幸福感”，沙坪坝区如火如荼地进行着社区环境的改善，提升老百姓的生活品质 $.$ 如图，某小区内有一块长为 $(3 a - b)$ 米，宽为 $(2 a + b)$ 米的长方形地块，小区计划在中间留一块边长为 $(a + b)$ 米的正方形地块修建一座假山，然后将剩余阴影部分进行绿化．

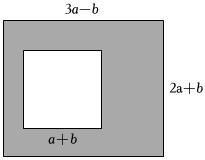(1)、求绿化部分的面积 $($ 用含 $a$ ， $b$ 的代数式表示 $)$ ；

(2)、当 $a = 3$ ， $b = 1$ 时，求绿化部分的面积．

查看试题解析
17. 如图，是由四个长为 $m$ ，宽为 $n$ 的小长方形拼成的正方形．

(1)、图中的阴影正方形的边长可表示为 $($ 用含 $m$ ， $n$ 的代数式表示 $)$ ；

(2)、根据图形中的数量关系，请你结合图形直接写出 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 之间的一个等量关系；

(3)、根据(2)中的结论，解决下列问题：若 $m + n = 7$ ， $m n = 3$ ，求阴影正方形的面积．

查看试题解析
18. 如图 $1$ 是一个长为 $4 a$ ，宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图 $2$ 的正方形．

(1)、由图 $2$ 可以直接写出 $(a + b)^{2}$ ， $(a - b)^{2}$ ， $a b$ 之间的一个等量关系是；

(2)、根据(1)中的结论，解决下列问题： $3 x + 4 y = 10$ ， $x y = 2$ ，求 $3 x - 4 y$ 的值；

(3)、两个正方形 $A B C D$ ， $A E F G$ 如图 $3$ 摆放，边长分别为 $x$ ， $y .$ 若 $x^{2} + y^{2} = 58$ ， $B E = 4$ ，求图中阴影部分面积和．

查看试题解析
19. 图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形．

(1)、图2中间空白的部分的面积是；

(2)、观察图2，请你写出代数式（a+b）²、（a-b）²、ab之间的等量关系式；

(3)、根据你得到的关系式解答下列问题：若x+y＝-4，xy＝3，求x-y的值．

查看试题解析

四、综合题

20. 若 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求m，n的值．
解：∵ $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，
∴ $(m^{2} - 2 m n + n^{2}) +$ （）=0，
即（）+（）=0．
根据非负数的性质，得m=n= ▲ ．

(1)、阅读上述解答过程，并补充横线处的内容；

(2)、设等腰三角形ABC的三边长分别为a，b，c，且满足 $a^{2} + b^{2} - 4 a - 6 b + 13 = 0$ ，求△ABC的周长．

查看试题解析
21. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，请解答下列问题：

(1)、写出图2中所表示的数学等式.

(2)、根据整式乘法的运算法则，通过计算验证上述等式.

(3)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 18$ ， $a^{2} + b^{2} + c^{2} = 116$ ，则 $a b + a c + b c =$ .

查看试题解析
22. 如图，在某高铁站广场前有一块长为 $2 a + b$ ，宽为 $a + b$ 的长方形空地，计划在中间留两个长方形喷泉池（图中阴影部分），两个长方形喷泉池及周边留有宽度为b的人行通道．

(1)、求该长方形空地的面积；（用代数式表示）

(2)、求这两个长方形喷泉池的总面积；（用代数式表示）

(3)、当 $a = 200$ ， $b = 100$ 时，求这两个长方形喷泉池的总面积．

查看试题解析
23. 阅读材料：
若x满足 $(9 - x) (x - 4) = 4$ ，求 $(9 - x)^{2} + (x - 4)^{2}$ 的值．

解：设 $9 - x = a$ ， $x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4$ ，

∴ $a + b = (9 - x) + (x - 4) = 5$ ，

∴ $(9 - x)^{2} + (x - 4)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ．

类比应用：

(1)、若 $(3 - x) (x - 2) = - 1$ ，求 $(3 - x)^{2} + (x - 2)^{2}$ 的值．

(2)、若 $(n - 2022)^{2} + (2023 - n)^{2} = 10$ ，则 $(n - 2022) (2023 - n)$ 的值为．

(3)、已知正方形 $A B C D$ 的边长为a，点P和点R分别是边 $A B$ 和 $C D$ 上的点，且 $A P = 4$ ， $C R = 2$ ，分别以 $B P$ 和 $D R$ 为边长作正方形 $P B E F$ 和正方形 $D M N R$ ．若图中阴影部分长方形的面积是4，则正方形 $P B E F$ 和正方形 $D M N R$ 的面积和为．

查看试题解析

（人教版）2023-2024学年八年级数学上册 14.2 乘法公式 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 14.2 乘法公式同步分层训练（提升卷）