（人教版）2023-2024学年八年级数学上册 14.1 整式的乘法同步分层训练（培优卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在长方形 $A B C D$ 中放入一个边长为8的大正方形 $A L M N$ 和两个边长为6的小正方形（正方形 $D E F G$ 和正方形 $H I J K$ ）.3个阴影部分的面积满足 $2 S_{3} + S_{1} - S_{2} = 2$ ，则长方形 $A B C D$ 的面积为（）

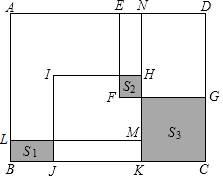A、90 B、96 C、98 D、100

查看试题解析
2. 若 $(x + m) (x - 1)$ 的计算结果中不含x的一次项，则m的值是（）

A、1 B、-1 C、2 D、-2．

查看试题解析
3. 如果单项式 $- 2 x^{4 a - b} y^{3}$ 与 $\frac{1}{2} x^{2} y^{a + b}$ 是同类项，这两个单项式的积是（）

A、 $x^{4} y^{6}$ B、 $- x^{2} y^{3}$ C、 $- \frac{3}{2} x^{2} y^{3}$ D、 $- x^{4} y^{6}$

查看试题解析
4. 下列整式运算正确的是（）

A、 $- 2 x^{2} \cdot 3 x = - 6 x^{2}$ B、 $2 x^{2} (- 3 x^{2} + 1) = - 6 x^{4} + 1$ C、 $(x + 2) (x + 1) = x^{2} + 3 x + 2$ D、 $x^{2} - 2 x (x - 1) = - x^{2} - 2 x$

查看试题解析
5. 如图，在一块长 $15 m$ ，宽 $12 m$ 的长方形空地上，修建同样宽的两条互相垂直的道路（两条道路各与长方形的一条边垂直），剩余部分栽种花草美化环境，设道路的管度为 $x m$ ，则栽种花草的面积表示不正确的是（）

A、 $(15 - x) (12 - x)$ B、 $15 \times 12 - 15 x - 12 x + x^{2}$ C、 $15 \times 12 - x (15 - x) - x (12 - x) - x^{2}$ D、 $(15 - x) (12 - x) + x^{2}$

查看试题解析
6. 若 $(x - 3) (x + 2) = x^{2} + m x + n$ ，则 $m ， n$ 的值分别是（）

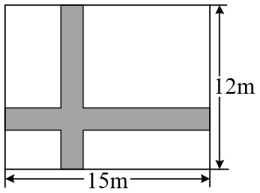A、 $- 1 ， - 6$ B、 $- 1 ， 6$ C、 $1 ， - 6$ D、1，6

查看试题解析
7. 计算：（-a²）³•a³结果为（　　）

A、-a⁹ B、a⁹ C、-a⁸ D、a⁸

查看试题解析
8. 已知 $4^{x} = 18 ， 8^{y} = 3$ ，则 $5^{2 x - 6 y}$ 的值为（）

A、5 B、10 C、25 D、50

查看试题解析
9. $8 a^{6} b^{4} c \div$ （） $= 4 a^{2} b^{2}$ ，则括号内应填的代数式（）

A、 $2 a^{3} b^{3} c$ B、 $2 a^{3} b^{2} c$ C、 $2 a^{4} b^{2} c$ D、 $\frac{1}{2} a^{4} b^{2} c$

查看试题解析
10. 已知 $(x - 4) (x - 9) = x^{2} + m x + 36$ ，则m的值为（）

A、 $- 13$ B、13 C、 $- 5$ D、5

查看试题解析

二、填空题

11. 如图，有5个形状大小完全相同的小长方形构造成一个大长方形（各小长方形之间不重叠且不留空隙），图中阴影部分的面积为32，则每个小长方形的对角线为．

查看试题解析
12. 现有A、B、C三种型号的地板砖，其规格如图所示，若用这三种地板砖铺设一个长为 $3 a + 2 b$ ，宽为 $a + b$ 的长方形地面，则需要B种地砖块．

查看试题解析
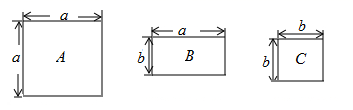13. 若（t-3）^t-2=1，则t=.

查看试题解析
14. 把3⁵⁵⁵ ， 4⁴⁴⁴ ， 5³³³由小到大用＜连接为．

查看试题解析
15. 若6^x=3，6^y=2，则6^2x^﹣^3y= ．

查看试题解析

三、解答题

16. 已知x⁷=2,y⁹=3,试比较x与y的大小.

查看试题解析
17. 已知（|x|﹣4）^x+1=1，求整数x的值.
小红与小明交流如下：

小红：因为a⁰=1（a≠0），

所以x+1=0且|x|﹣4=0，所以x=﹣1．

小明：因为1ⁿ=1，所以|x|﹣4=1，所以x=±5

你认为小红与小明同学的解答完整吗？若不完整，请求出其他所有的整数x的值．

查看试题解析
18. 如果关于 $x$ 的多项式 $x - 2$ 与 $x^{2} + m x + 1$ 的乘积中不含 $x$ 的一次项，求 $m$ 的值．

查看试题解析
19. 如图，有一块长方形纸板，长是宽的2倍，要将其四角各剪去一个正方形，折成一个无盖的长方体盒子（纸板厚度忽略不计）．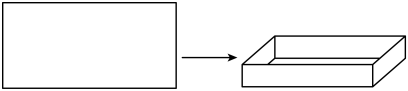

(1)、请在图中的长方形纸板上画出示意图，用实线表示剪切线，虚线表示折痕．

(2)、已知剪去的小正方形的边长为 $2 c m$ ，设长方形纸板的宽为 $x c m$ ，求折成的长方体盒子的容积．

(3)、实际测量知，长方形纸板的长为 $20 c m$ ，请在（2）的条件下计算折成的长方体盒子的容积．

查看试题解析

四、综合题

20. 已知多项式 $x + 3$ 与另一个多项式 $A$ 的乘积为多项式 $B$ ．

(1)、若 $A$ 为关于 $x$ 的一次多项式 $x + a$ ， $B$ 为关于 $x$ 的二次二项式，求 $a$ 的值；

(2)、若 $B$ 为 $x^{3} + p x^{2} + q x + 6$ ，求 $3 p - q$ 的值．

查看试题解析
21. 在我国南宋数学家杨辉（约13世纪）所著的《详解九章算术》（1261年）一书中，用下图的三角形解释二项和的乘方规律．杨辉在注释中提到，在他之前北宋数学家贾宪（1050年左右）也用过上述方法，因此我们称这个三角形为“杨辉三角”或“贾宪三角”．杨辉三角两腰上的数都是 $1$ ，其余每一个数为它上方（左右）两数的和．事实上，这个三角形给出了 ${(a + b)}^{n}$ $(n = 1 ， 2 ， 3 ， 4 ， 5 ， 6 \dots)$ 的展开式（按 $a$ 的次数由大到小的顺序）的系数规律．例如，此三角形中第三行的 $3$ 个数 $1 ， 2 ， 1$ ，恰好对应着 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 展开式中的各项系数，第四行的 $4$ 个数 $1 ， 3 ， 3 ， 1$ ，恰好对应着 ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ 展开式中的各项系数，等等．请依据上面介绍的数学知识，解决下列问题：

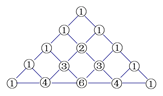(1)、写出 ${(a + b)}^{4}$ 的展开式；

(2)、利用整式的乘法验证你的结论．

查看试题解析
22. 基本事实：若 $a^{m} = a^{n}$ （a>0，且a≠1，m ， n都是正整数），则m=n.试利用上述基本事实解决下面的两个问题：

(1)、如果 $2 \times 8^{x} \times 16^{x} = 2^{22}$ ，求x的值．

(2)、如果 $2^{x + 1} • 2 + 2^{x + 1} = 24$ ，求x的值．

查看试题解析
23. （知识回顾）
七年级学习代数式求值时，遇到这样一类题“代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式= $(a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，则 $a = - 3$ .

(1)、（理解应用）
若关于x的多项式 $(2 x - 3) m + 2 m^{2} - 3 x$ 的值与x的取值无关，求m值；

(2)、已知 $A = (2 x + 1) (x - 1) - x (1 - 3 y)$ ， $B = - x^{2} + x y - 1$ ，且3A+6B的值与x无关，求y的值；

(3)、（能力提升）
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分(图中阴影部分)，设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求a与b的等量关系.

查看试题解析

（人教版）2023-2024学年八年级数学上册 14.1 整式的乘法 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 14.1 整式的乘法同步分层训练（培优卷）