(人教版)2023-2024学年八年级数学上册 13.4 课题学习 最短路径问题 同步分层训练(基础卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
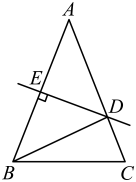
1. 如图,中, , 垂直平分 , 点P为直线上一动点,则的最小值为( )
 A、3 B、5 C、6 D、72. 如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A、3 B、5 C、6 D、72. 如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( ) A、2 B、4 C、6 D、83. 数学课上,老师提出如下问题:
A、2 B、4 C、6 D、83. 数学课上,老师提出如下问题:如图1,点P、Q是直线l同侧的两点,请你在直线l上确定一个点R.使 的周长最小.小明的作法如下,如图2:
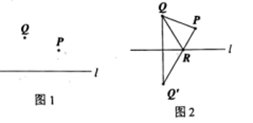
( 1 )作点Q关于直线l的对称点 ;
( 2 )连接 ,交直线l于点R;
( 3 )连接RQ、PQ.
那么点R就是使 的周长最小的点.
老师说,小明的做法正确.接着.老师问同学们,小明这种作法应用了哪些我们学过的定理呢?有四位同学分别说了一个定理,下面的A,B,C,D四个答案分别代表了四个同学所说的定理,其中小明没有应用到的定理是( )
A、如果两个图形关于某直线对称,那么对称轴是对称点连线的垂直平分线 B、等腰三角形底边上的高也是顶角的角平分线 C、线段垂直平分线上的点到线段两个端点的距离相等 D、两点之间,线段最短4. 如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是( )A、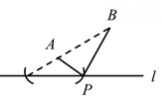 B、
B、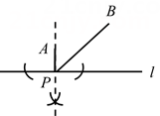 C、
C、 D、
D、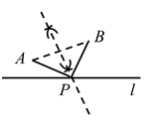 5. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )
5. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )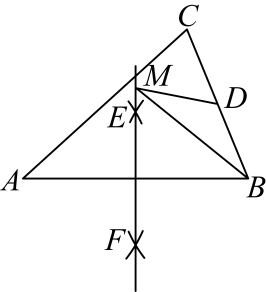 A、 B、 C、 D、6. 如图,四边形是直角梯形, , , 点是腰上的一个动点,要使最小,则点应该满足( )
A、 B、 C、 D、6. 如图,四边形是直角梯形, , , 点是腰上的一个动点,要使最小,则点应该满足( ) A、 B、 C、 D、7. 如图,平分 , 点P是射线上一点,于点M , 点N是射线上的一个动点.若 , 则的长度不可能是( )
A、 B、 C、 D、7. 如图,平分 , 点P是射线上一点,于点M , 点N是射线上的一个动点.若 , 则的长度不可能是( ) A、5 B、6 C、7 D、48. 如图,是等边三角形,D,E分别是边的中点,连接 , 点P是上一动点,若 , 则的最小值是( )
A、5 B、6 C、7 D、48. 如图,是等边三角形,D,E分别是边的中点,连接 , 点P是上一动点,若 , 则的最小值是( ) A、2 B、4 C、8 D、169. 如图,河道l的同侧有M , N两个村庄,计划铺设管道将河水引至M , N两村,下面四个方案中,管道总长度最短的是( )
A、2 B、4 C、8 D、169. 如图,河道l的同侧有M , N两个村庄,计划铺设管道将河水引至M , N两村,下面四个方案中,管道总长度最短的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,是等边三角形,是边上的高,点E是边的中点,点P是上的一个动点,当最小时,的度数是( )
10. 如图,是等边三角形,是边上的高,点E是边的中点,点P是上的一个动点,当最小时,的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,直线与轴、轴分别交于点和点 , 点、分别为线段、的中点,点为上一动点,当最小时,点的坐标为 .
 12. 如图,已知△ABC为等边三角形,高AH=8cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为cm.
12. 如图,已知△ABC为等边三角形,高AH=8cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为cm. 13. 如图,在△ABC中,AB=6,AC=8,AB⊥AC,MN垂直平分BC,点P为直线MN上一动点,则AP+BP的最小值是.
13. 如图,在△ABC中,AB=6,AC=8,AB⊥AC,MN垂直平分BC,点P为直线MN上一动点,则AP+BP的最小值是. 14. 如图,一束光线从y轴上的点A(0,1)出发,经过x轴上的点C反射后经过点B(6,2),则光线从A点到B点经过的路线长度为 .
14. 如图,一束光线从y轴上的点A(0,1)出发,经过x轴上的点C反射后经过点B(6,2),则光线从A点到B点经过的路线长度为 . 15. 如图,在中, , 垂直平分 , 点P为直线上的任一点,则的最小值是 .
15. 如图,在中, , 垂直平分 , 点P为直线上的任一点,则的最小值是 .
三、解答题
-
16. 如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程.
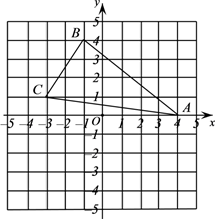
 17. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
17. 如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).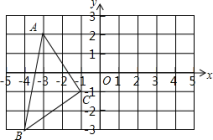
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
18. 某高速公路的同一侧有A,B两个城镇,如图所示,它们到高速公路所在直线 的距离分别为 , , ,要在高速公路上E、F之间建一个出口Q,使A、B两城镇到Q的距离之和最短,在图中画出点Q所在位置,并求出这个最短距离. 19. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小.
19. 已知:如图,点M在锐角∠AOB的内部,在OA边上求作一点P , 在OB边上求作一点Q , 使得△PMQ的周长最小.
四、综合题
-
20. 如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
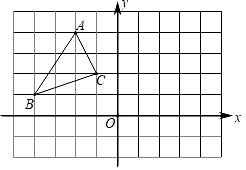
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
21. 如图,在平面直角坐标系中,的顶点都在网格格点上,点坐标为 . (1)、作出关于轴对称的 , 并写出点的坐标;(2)、在轴上找一点 , 使得最短,并写出点的坐标.
(1)、作出关于轴对称的 , 并写出点的坐标;(2)、在轴上找一点 , 使得最短,并写出点的坐标.