备考2024年浙江中考数学一轮复习专题2.2无理数与实数真题集训

试卷更新日期：2023-11-06 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在 $- 2 ， - 1 ， 0 ， π$ 这四个数中，最小的数是（）

A、 $- 2$ B、 $- 1$ C、0 D、 $π$

查看试题解析
2. -8的立方根是（）

A、 $- 2$ B、2 C、 $\pm 2$ D、不存在

查看试题解析
3. 如图，数轴上的A、B、C、D四点中，与数﹣ $\sqrt{3}$ 表示的点最接近的是（）

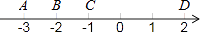A、点A B、点B C、点C D、点D

查看试题解析
4. 下列无理数中，大小在3与4之间的是（）．

A、 $\sqrt{7}$ B、 $2 \sqrt{2}$ C、 $\sqrt{13}$ D、 $\sqrt{17}$

查看试题解析
5. 一个正方形的面积是15，估计它的边长大小在（）

A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间

查看试题解析
6. 大小在 $\sqrt{2}$ 和 $\sqrt{5}$ 之间的整数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 能说明命题“若x为无理数，则x²也是无理数”是假命题的反例是（）

A、x＝ $\sqrt{2}$ ﹣1 B、x＝ $\sqrt{2}$ +1 C、x＝3 $\sqrt{2}$ D、x＝ $\sqrt{3}$ ﹣ $\sqrt{2}$

查看试题解析
8. 下面四个数中，比1小的正无理数是（）

A、 $\frac{\sqrt{6}}{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、 $\frac{1}{3}$ D、 $\frac{π}{3}$

查看试题解析
9. 已知 $a$ ， $b$ 是两个连续整数， $a < \sqrt{3} - 1 < b$ ，则 $a$ ， $b$ 分别是（）

A、-2，-1 B、-1，0 C、0，1 D、1，2

查看试题解析
10. 下列说法正确的是（）

A、 $\frac{\sqrt{2}}{2}$ 是分数 B、16的平方根是±4，即 $\sqrt{16} = \pm 4$ C、8.30万精确到百分位 D、若 $\sqrt{a - 2022} + | b + 1 | = 0$ ，则 $b^{a} = 1$

查看试题解析

二、填空题（每题4分，共24分）

11. 计算： $2 \times 2^{- 1}$ =

查看试题解析
12. 若一个数的平方等于5，则这个数等于。

查看试题解析
13. 实数 $- 8$ 的立方根是

查看试题解析
14. 把7的平方根和立方根按从小到大的顺序排列为．

查看试题解析
15. 请写出一个小于4的无理数：

查看试题解析
16. 任何实数a，可用[a]表示不超过a的最大整数，如[4]=4，[ $\sqrt{3}$ ]=1．现对72进行如下操作：72 $\overset{第一次}{\to}$ [ $\sqrt{72}$ ]=8 $\overset{第二次}{\to}$ [ $\sqrt{8}$ ]=2 $\overset{第三次}{\to}$ [ $\sqrt{2}$ ]=1，这样对72只需进行3次操作后变为1，类似的，①对81只需进行次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是．

查看试题解析

三、计算题（共2题，共18分）

17. 计算：

(1)、 $| - 1 | + \sqrt[3]{- 8} + {(\frac{1}{3})}^{- 2} - (- 4)$ .

(2)、 $\frac{a^{2} + 2}{a + 1} - \frac{3}{1 + a}$ .

查看试题解析
18. 计算： $(- 2023)^{0} + \sqrt{4} - 2 s i n 30 ° + | - 5 |$ .

查看试题解析

四、解答题（共2题，共28分）

19. 如图1，把两个边长为1的小正方形沿对角线剪开，所得的4个直角三角形拼成一个面积为2的大正方形．由此得到了一种能在数轴上画出无理数对应点的方法．

(1)、图2中A、B两点表示的数分别为，；

(2)、请你参照上面的方法：
①把图3中 $5 \times 1$ 的长方形进行剪裁，并拼成一个大正方形．在图3中画出裁剪线，并在图4的正方形网格中画出拼成的大正方形，该正方形的边长 $a =$ ．（注：小正方形边长都为1，拼接不重叠也无空隙）

②在①的基础上，参照图2的画法，在数轴上分别用点M、N表示数a以及 $a - 3$ ．（图中标出必要线段的长）

查看试题解析
20. 如图1，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形.

(1)、拼成的正方形的面积与边长分别是多少？

(2)、如图2所示，以数轴的单位长度的线段为边作一个直角三角形，以数轴的﹣1点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A，那么点A表示的数是多少？点A表示的数的相反数是多少？

(3)、如图3你能把十三个小正方形组成的图形纸，剪开并拼成正方形吗？若能，请画出示意图，并求它的边长是多少？

查看试题解析

备考2024年浙江中考数学一轮复习专题2.2无理数与实数 真题集训

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、计算题（共2题，共18分）

四、解答题（共2题，共28分）

备考2024年浙江中考数学一轮复习专题2.2无理数与实数真题集训