（人教版）2023-2024学年八年级数学上册 13.3 等腰三角形 同步分层训练（基础卷）
试卷更新日期：2023-11-06 类型：同步测试
一、选择题
-
1. 已知一个等腰三角形的两边长分别是4，5，则它的周长是（ ）A、13 B、14 C、9或12 D、13或142. 等腰三角形的两边分别为3和6，则这个三角形的周长是（ ）A、9 B、12 C、15 D、12或153. 如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）
A、 B、 C、 D、4. 已知等腰三角形的一个内角为 ， 则它的底角为（ ）A、 B、 C、或 D、或5. 已知等腰三角形ABC的一个角为80°，则该三角形的顶角为（ ）A、80° B、20° C、80°或20° D、以上都不对6. 在△ABC中，AC＝BC，CD为AB边上的高，∠ACB＝92°，则∠ACD的度数为（ ）
A、45° B、46° C、50° D、60°7. 如图，在ABC中，AB＝AC，AD平分∠BAC，则下列结论错误的是（ ）
A、∠B＝∠C B、AD⊥BC C、∠BAD＝∠CAD＝∠C D、BD＝CD8. 在中， ， ， 则的长为（ ）A、1 B、2 C、3 D、49. 如图，在中， ， ， 则的长为（ ）
A、2 B、3 C、4 D、510. 如图， ， ， 则等于（ ）
A、 B、 C、 D、二、填空题
-
11. 已知等腰三角形的一边长为3，另一边长为6，则它的周长为.12. 若等腰三角形的一个内角为 ， 则底角为.13. 一张小凳子的结构如图所示，AC=BC，∠1=100°， 则∠2=°．
14. 一个等腰三角形有一个角为 ， 则它的顶角度数为15. 如图，在△ABC中，AB＝AC，且D为BC上一点，CD＝AD，AB＝BD，则∠B的度数为.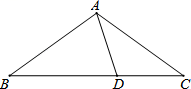
三、解答题
-
16. 如图，点D、E在的边上， ， ， 求证：.
17. 如图，在中， ， D是边上的中点，于点E，于点F.求证：点D在的角平分线上.
18. 如图，在△ABC中，AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝130°，求∠BAC的度数.
19. 如图， ， ， ， 平分 ， 若 ， 求的长.
四、综合题
-
20. 如图，在 中， ， 于点 ， 平分 交 于点 ．
(1)、求证： ；(2)、若 ， ，求 的长．21. 已知：如图， ，
(1)、求证：(2)、求证：22. 如图，AB∥CD，直线 EF 分别交 AB、CD于 点 E、F，EG 平分∠AEF，
(1)、求证：△EGF 是等腰三角形．(2)、若∠1=40°，求∠2 的度数．23. 如图，△ABC中，AB=BC=AC=12cm，现有两点M、N分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M、N同时停止运动．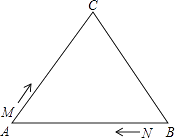
(1)、点M、N运动几秒后，M、N两点重合？(2)、点M、N运动几秒后，可得到等边三角形△AMN？(3)、当点M、N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M、N运动的时间．