(人教版)2023-2024学年八年级数学上册 13.3 等腰三角形 同步分层训练(提升卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
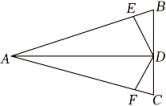
1. 若三角形的重心在它的一条高线上,则这个三角形一定是( ).A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形2. 如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法中正确的有( )
①AD平分∠EDF;②△EBD≌△FCD;③BD=CD;④AD⊥BC.
 A、1个 B、2个 C、3个 D、4个3. 如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G,连结DG,EG.添加下列条件,不能使BG=CG成立的是( )
A、1个 B、2个 C、3个 D、4个3. 如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G,连结DG,EG.添加下列条件,不能使BG=CG成立的是( )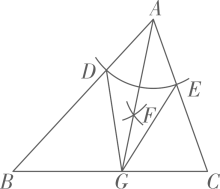 A、 B、 C、 D、4. 等腰三角形一边长为 , 一边长为 , 则它的周长等于( )A、16 B、17 C、16或17 D、以上都不对5. 如图,在中, , , 点是延长线上一点,过点作
A、 B、 C、 D、4. 等腰三角形一边长为 , 一边长为 , 则它的周长等于( )A、16 B、17 C、16或17 D、以上都不对5. 如图,在中, , , 点是延长线上一点,过点作
则的度数为( ) A、
A、
B、
C、
D、6. 如图,在△ABC中,∠BAC=80°,交BC于点E,边AC的垂直平分线交AC于点F,连接AE,AG.则∠EAG的度数为( ) A、35° B、30° C、25° D、20°7. 如图,在中,按以下步骤作图:分别以 , 为圆心,大于的长为半径作弧,两弧相交于 , 两点;作直线交于点 , 连接若 , , 则的度数为( )
A、35° B、30° C、25° D、20°7. 如图,在中,按以下步骤作图:分别以 , 为圆心,大于的长为半径作弧,两弧相交于 , 两点;作直线交于点 , 连接若 , , 则的度数为( ) A、 B、 C、 D、8. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )
A、 B、 C、 D、8. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )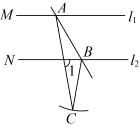 A、 B、 C、 D、9. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
A、 B、 C、 D、9. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
;
点在的垂直平分线上;
图中共有个等腰三角形;
≌;
其中正确的结论有( )
A、个 B、个 C、个 D、个10. 如图所示,点E到△ABC三边的距离相等,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=2019,则线段NM的长为( ) A、2017 B、2018 C、2019 D、2020
A、2017 B、2018 C、2019 D、2020二、填空题
-
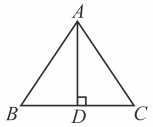
11. 等腰三角形的两边长分别为、 , 它的周长为 .12. 如图,已知在中, , 于点D , 若 , 则的度数为 .
 13. 如图,是线段上的一点,和都是等边三角形,交于 , 交于 , 交于 , 则①;②;③;④ . 其中,正确的有 .
13. 如图,是线段上的一点,和都是等边三角形,交于 , 交于 , 交于 , 则①;②;③;④ . 其中,正确的有 . 14. 一个等腰三角形的两边长分别为 , , 则它的周长为 .15. 若等腰三角形一腰上的高和另一腰的夹角为20°,则该三角形的一个底角为°
14. 一个等腰三角形的两边长分别为 , , 则它的周长为 .15. 若等腰三角形一腰上的高和另一腰的夹角为20°,则该三角形的一个底角为°三、解答题
-
16. 如图,是等边三角形,延长至点 , 将点关于直线对称得到点 , 延长线段至点使得 , 连接 , , , , 记线段交直线于点 , 线段交直线于点 , 连接请你补全图形,判断的形状,并证明你的结论.
 17. 如图,在中,点是中点, , , 且求证:是等腰三角形.
17. 如图,在中,点是中点, , , 且求证:是等腰三角形. 18. 如图,在中, , , 于点D,于点E, , 求的长.
18. 如图,在中, , , 于点D,于点E, , 求的长.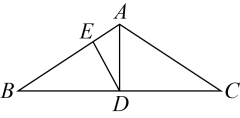 19. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
19. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
四、综合题
-
20. 如图,在△ABC中,AB=AC,点D是BC的中点,连接AD,过点C作CE∥AD,交BA的延长线于点E.
 (1)、求证:EC⊥BC;(2)、若∠BAC=120°,试判定△ACE的形状,并说明理由.
(1)、求证:EC⊥BC;(2)、若∠BAC=120°,试判定△ACE的形状,并说明理由.