(人教版)2023-2024学年八年级数学上册 13.3 等腰三角形 同步分层训练(培优卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 如图,△ABC中,AD是它的角平分线,P是AD上的一点,PE∥AB交BC于点E,PF∥AC交BC于点F,G为EF的中点,若PE=3,PF=6,则S△PED:S△PDG=( )
 A、 B、 C、 D、2. 如图,AD是的角平分线,DE⊥AC,垂足为E,交ED的延长线于点F,若DE=DF,AE=2BF.下列四个结论:①BC平分∠ABF;②;③AD⊥BC;④AB=3BF.其中正确的结论有( )
A、 B、 C、 D、2. 如图,AD是的角平分线,DE⊥AC,垂足为E,交ED的延长线于点F,若DE=DF,AE=2BF.下列四个结论:①BC平分∠ABF;②;③AD⊥BC;④AB=3BF.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个3. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A、1个 B、2个 C、3个 D、4个3. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )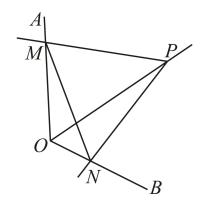 A、的值不变 B、 C、的长不变 D、四边形的面积不变4. 如图,已知与都是等边三角形,点B,C,D在同一条直线上,与相交于点 , 与相交于点 , 与相交于点 , 则下列结论:①;②;③;④是等边三角形,其中正确的个数是( )
A、的值不变 B、 C、的长不变 D、四边形的面积不变4. 如图,已知与都是等边三角形,点B,C,D在同一条直线上,与相交于点 , 与相交于点 , 与相交于点 , 则下列结论:①;②;③;④是等边三角形,其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个5. 如图,在中, , 边的垂直平分线交于点D,交于点E,边的垂直平分线交于点F,交于点G,连接 , . 则的度数( )
A、1个 B、2个 C、3个 D、4个5. 如图,在中, , 边的垂直平分线交于点D,交于点E,边的垂直平分线交于点F,交于点G,连接 , . 则的度数( )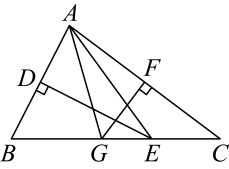 A、 B、 C、 D、6. 如图,在中,的高BD、CE交于点 , 若 , 则AC的长为( )
A、 B、 C、 D、6. 如图,在中,的高BD、CE交于点 , 若 , 则AC的长为( ) A、18 B、20 C、22 D、247. 已知点在第一象限,若在轴上确定点使得为等腰三角形,则点的坐标有( )种可能A、3 B、4 C、1或3 D、2或48. 如图,⊙O的半径为r,交×轴正半轴于点A,直线l垂直平分OA交⊙O于点P,PB⊥y轴于点B.今假设在点O,A处,分别有一质量为m1 , m2的天体(m1>m2);天体物理中把与O,A处于同一平面,坐标为( , )的点称为[O,A]系统的拉格朗日4号点,记为L4 (若把卫星发射到L4的位置,则卫星会处于相对静止的稳状态).以下说法中错误的是( )
A、18 B、20 C、22 D、247. 已知点在第一象限,若在轴上确定点使得为等腰三角形,则点的坐标有( )种可能A、3 B、4 C、1或3 D、2或48. 如图,⊙O的半径为r,交×轴正半轴于点A,直线l垂直平分OA交⊙O于点P,PB⊥y轴于点B.今假设在点O,A处,分别有一质量为m1 , m2的天体(m1>m2);天体物理中把与O,A处于同一平面,坐标为( , )的点称为[O,A]系统的拉格朗日4号点,记为L4 (若把卫星发射到L4的位置,则卫星会处于相对静止的稳状态).以下说法中错误的是( ) A、△AOP是等边三角形 B、L4在线段BP上 C、∠OL4A>60° D、若m1恒定,则m2越小,L4离点P越近9. 如图,在平面直角坐标系中,点在轴的正半轴上,在第一象限,且△是等边三角形.在射线上取点 , , , 分别以 , , 为边作等边三角形△ , △ , 使得 , , , 在同一直线上,该直线交轴于点.若 , , 则点的横坐标是( )
A、△AOP是等边三角形 B、L4在线段BP上 C、∠OL4A>60° D、若m1恒定,则m2越小,L4离点P越近9. 如图,在平面直角坐标系中,点在轴的正半轴上,在第一象限,且△是等边三角形.在射线上取点 , , , 分别以 , , 为边作等边三角形△ , △ , 使得 , , , 在同一直线上,该直线交轴于点.若 , , 则点的横坐标是( ) A、 B、 C、256 D、10. 如图,为的角平分线, , 过作于 , 交的延长线于 , 则下列结论:
A、 B、 C、256 D、10. 如图,为的角平分线, , 过作于 , 交的延长线于 , 则下列结论:①;②;③;④ .
其中正确结论的序号有( )
 A、①②③④ B、②③④ C、①②③ D、①②④
A、①②③④ B、②③④ C、①②③ D、①②④二、填空题
-
11. 在△ABC中,AB=AC,且过△ABC某一顶点的直线可将△ABC分成两个等腰三角形,则∠BAC的度数为 .12. 如图,C是线段AB上的一点,和都是等边三角形,AE交CD于M , BD交CE于N , 交AE于 , 则①;②;③;④;⑤是等边三角形.其中,正确的有 .
 13. 如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=度.
13. 如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=度. 14. 如图,已知Rt△ABC , AB=AC , 将边AB绕着点A旋转,当点B落在边AB的垂直平分线上的点E时,∠AEC=.
14. 如图,已知Rt△ABC , AB=AC , 将边AB绕着点A旋转,当点B落在边AB的垂直平分线上的点E时,∠AEC=.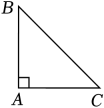 15. 在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A , C重合),且∠ABP=30°,则CP的长为 .
15. 在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A , C重合),且∠ABP=30°,则CP的长为 .三、解答题
-
16. 如图,在中, , 平分 , 于 , 若 , 求的度数.
 17. 平面直角坐标系中,已知 , 为等腰三角形且面积为 , 求满足条件的点坐标.
17. 平面直角坐标系中,已知 , 为等腰三角形且面积为 , 求满足条件的点坐标. 18. 小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
18. 小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②). 19. 如图所示,AB∥CD,EF= EH,EH平分∠AEG,且∠EHF=15° ,求∠CFH的度数.
19. 如图所示,AB∥CD,EF= EH,EH平分∠AEG,且∠EHF=15° ,求∠CFH的度数.
四、综合题
-
20. 如图,和均为等边三角形.
 (1)、找出与全等的三角形(不需要说明理由);(2)、若 , 求的度数.21. 在等边三角形中,D为射线上一点,连接 , 点B关于直线的对称点为E,连接 .
(1)、找出与全等的三角形(不需要说明理由);(2)、若 , 求的度数.21. 在等边三角形中,D为射线上一点,连接 , 点B关于直线的对称点为E,连接 . (1)、如图1,点D在线段上, , 求的度数;(2)、射线与射线的交于点F,过点D作交射线于点G,连接交于点H.
(1)、如图1,点D在线段上, , 求的度数;(2)、射线与射线的交于点F,过点D作交射线于点G,连接交于点H.①如图2,点D在线段上,求证:;
②点D在线段延长线上,用等式表示线段和之间的数量关系,并说明理由.
22. 如图,在中, , , , 交CA的延长线于点D,BE平分交CD于点E,点F在BD延长线上, , 连接FE并延长交BC于点H. (1)、求的度数;(2)、如图,延长BA到点G,使 , 连接EG.判断BH和EH的位置关系,并说明理由.23. 已知是等边三角形.
(1)、求的度数;(2)、如图,延长BA到点G,使 , 连接EG.判断BH和EH的位置关系,并说明理由.23. 已知是等边三角形. (1)、如图1,点D是边的中点,点P为射线AC上一动点,当是轴对称图形时,的度数为;(2)、如图2, , 点D在边上,点F在射线上,且 , 作于G,当点D在边上移动时,请同学们探究线段 , , 之间有什么数量关系,并对结论加以证明;(3)、如图3,点R在延长线上,连接 , S为上一点, , 连接交于T,若 , , 直接写出线段的值为 .
(1)、如图1,点D是边的中点,点P为射线AC上一动点,当是轴对称图形时,的度数为;(2)、如图2, , 点D在边上,点F在射线上,且 , 作于G,当点D在边上移动时,请同学们探究线段 , , 之间有什么数量关系,并对结论加以证明;(3)、如图3,点R在延长线上,连接 , S为上一点, , 连接交于T,若 , , 直接写出线段的值为 .