（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形同步分层训练（培优卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，正方形ABCD的顶点A(1，1)，B(3， 1)，规定把正方形ABCD“先沿x轴进行翻折，再向左平称1个单位”为一次变换，这样连续经过2021次变换后，正方形ABCD的顶点C的坐标为（）

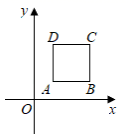A、(-2018，3) B、(-2018，-3) C、(-2019，3) D、(-2019， -3)

查看试题解析
2. 已知点E（x₀ ， y_o），点F（x₂.y₂），点M（x₁ ， y₁）是线段EF的中点，则x₁＝ $\frac{x_{0} + x_{2}}{2}$ ，y₁＝ $\frac{y_{0} + y_{2}}{2}$ .在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P₁（即P，A，P₁三点共线，且PA＝P₁A），P₁关于点B的对称点P₂ ， P₂关于点C的对称点P₃ ， …按此规律继续以A，B，C三点为对称点重复前面的操作.依次得到点P₄ ， P₅ ， P₆…，则点P₂₀₂₀的坐标是（　　）

A、（4，0） B、（﹣2，2） C、（2，﹣4） D、（﹣4，2）

查看试题解析
3. 在平面直角坐标系中，正方形ABCD的顶点分别为A（1，1）.B（1，﹣1）.C（﹣1，﹣1）.D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P₁ ，作P₁关于点B的对称点P₂ ，作点P₂关于点C的对称点P₃ ，作P₃关于点D的对称点P₄ ，作点P₄关于点A的对称点P₅ ，作P₅关于点B的对称点P₆┅，按如此操作下去，则点P₂₀₁₁的坐标为（）

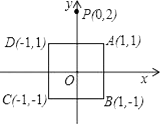A、（0，2） B、（2，0） C、（0，﹣2） D、（﹣2，0）

查看试题解析
4.
如图，直线l₁与直线l₂相交，∠α＝60°，点P在∠α内（不在l₁ ， l₂上）。小明用下面的方法作P的对称点：先以l₁为对称轴作点P关于l₁的对称点P₁ ，再以l₂为对称轴作P₁关于l₂的对称点P₂ ，然后再以l₁为对称轴作P₂关于l₁的对称点P₃ ，以l₂为对称轴作P₃关于l₂的对称点P₄ ， ……，如此继续，得到一系列点P₁ ， P₂ ， P₃ ， …，P_n。若P_n与P重合，则n的最小值是（）

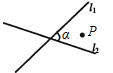A、5 B、6 C、7 D、8

查看试题解析
5. 如图，在平面直角坐标系中点A的坐标为（3，4），D是△ABC内一点，将△ABC平移得到 $△ A^{'} B^{'} C^{'}$ ，平移后点D与其对应点D'关于x轴对称，设点D的坐标为（a，b），则A的对应点 $A^{'}$ 的坐标为（）

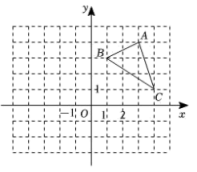A、（3，－4） B、（3，4－2b） C、（3，4－2a） D、（－3，4－2b）

查看试题解析
6. 若坐标平面上点P(a，1)与点Q(-4，b)关于x轴对称，则（）

A、a=4，b=-1 B、a=-4，b=1 C、a=-4，b=-1 D、a=4，b=1

查看试题解析
7. 若点 $A (a ， - 2)$ ， $B (3 ， b)$ 关于x轴对称，则a ， b的值分别为（）

A、 $a = 3$ ， $b = - 2$ B、 $a = - 3$ ， $b = - 2$ C、 $a = 3$ ， $b = 2$ D、 $a = - 3$ ， $b = 2$

查看试题解析
8. 将 $△ A B C$ 的三个顶点的纵坐标不变，横坐标均乘以 $- 1$ 后得到 $△ D E F$ ，则 $△ D E F$ （）．

A、与 $△ A B C$ 关于x轴对称 B、与 $△ A B C$ 关于y轴对称 C、与 $△ A B C$ 关于原点对称 D、向x轴的负方向平移了一个单位

查看试题解析
9. 平面直角坐标系中，若点 $A (- 1 ， a)$ 与点 $B (b ， 3)$ 关于x轴对称，则点 $C (a ， b)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 已知点 $A (a ， 1)$ 与点 $A' (5 ， b)$ 关于 $y$ 轴对称，则代数式 $a + b$ 值为（）

A、-6 B、6 C、4 D、-4

查看试题解析

二、填空题

11. 已知点M的坐标为 $(- 4 ， 2)$ ，则M关于原点对称的点的坐标为．

查看试题解析
12. 已知点 $A (- 1 ， a + 1)$ ， $B (b ， - 3)$ 是关于x轴对称的点， $a - b =$ ．

查看试题解析
13. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

查看试题解析
14. 已知点M（x，y）与点N（﹣2，﹣3）关于x轴对称，则x+y= ．

查看试题解析
15. 已知点A（5，0），点A关于直线y=kx（k＞0）的对称点B正好落在反比例函数y= $\frac{12}{x}$ 第一象限的图象，则k= ．

查看试题解析

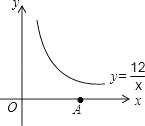
三、解答题

16. 如果△ABC关于x轴进行轴对称变换后，得到△A₁B₁C₁ ，而△A₁B₁C₁关于y轴进行轴对称变换后，得到△A₂B₂C₂ ，若△ABC三个顶点坐标分别为A（-2，3）、B（-4，2）、C（-1，0），请你分别写出△A₁B₁C₁与△A₂B₂C₂各顶点坐标．

查看试题解析
17. 已知如图，点P在 $∠ A O B$ 内，请按要求完成以下问题．

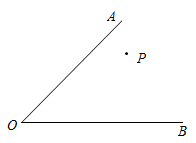(1)、分别作P关于OA、OB的对称点M、N，连结MN分别交OA、OB于E、F；

(2)、若 $△ P E F$ 的周长为20，求MN的长．

查看试题解析
18. 已知点 $A (2 a - b ， 5 + a)$ ， $B (2 b - 1 ， - a + b)$ .若 $A$ 、 $B$ 关于 $y$ 轴对称，求 ${(4 a + b)}^{2020}$ 的值．

查看试题解析
19. 如图在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 3 ， 4)$ ， $B (- 4 ， 1)$ ， $C (- 1 ， 1)$

(1)、请在图中画出 $△ A B C$ 关于 $y$ 轴的对称图形 $△ A^{'} B^{'} C^{'}$ ，点 $A$ 、 $B$ 、 $C$ 的对称点分别为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ ，其中 $A^{'}$ 的坐标为； $B^{'}$ 的坐标为； $C^{'}$ 的坐标为．

(2)、请求出 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析

四、综合题

20. 已知 $∠ A O B = 30 °$ ，点P在 $∠ A O B$ 的内部，点C和点P关于OA对称，点P关于OB的对称点是D，连接CD交OA于M，交OB于N， $C D = 15$ ．

(1)、补全图，并且保留作图痕迹．

(2)、写出∠COD°．△PMN的周长为．

查看试题解析
21. 如图， $O$ 为 $△ A B C$ 内部一点， $P$ 、 $R$ 分别为点 $O$ 关于直线 $A B$ 、 $B C$ 对称的点．

(1)、若 $∠ A B C = 60 °$ ，求 $∠ P O R$ 的度数；

(2)、试猜想当 $P R$ 的值最大时， $∠ A$ 与 $∠ C$ 需要满足什么数量关系，并说明理由．

查看试题解析
22. 如图所示，△ABC的顶点分别为A（-4， 5），B（﹣3， 2），C（4，-1）．

(1)、作出△ABC关于x轴对称的图形△A₁B₁C₁；

(2)、写出A₁、B₁、C₁的坐标；

(3)、若AC=10，求△ABC的AC边上的高．

查看试题解析
23. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

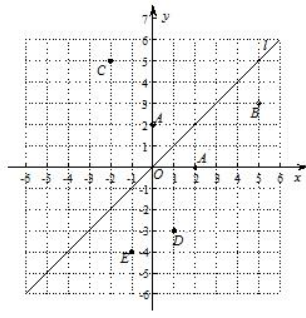(1)、实验与探究：
由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B(5，3)、C(-2，5)关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′、C′；

(2)、归纳与发现：
结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a，b)关于第一、三象限的角平分线l的对称点P′的坐标为（不必证明）；

(3)、运用与发现：
已知两点D(1，-3)、E(-1，-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小.

查看试题解析

（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形同步分层训练（培优卷）