（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形同步分层训练（提升卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 若点(3，a-2)与点(b+2，-1)关于原点对称，则点(a，b)位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在平面直角坐标系中，点 $P (- 1 ， 2)$ 关于原点的对称点的坐标是（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(2 ， - 1)$ D、 $(1 ， - 2)$

查看试题解析
3. 若直线l与直线y＝2x-3关于y轴对称，则直线l的解析式是（　　）

A、y＝-2x+3 B、y＝-2x-3 C、y＝2x+3 D、y＝2x-3

查看试题解析
4. 在平面直角坐标系中，把△ABC先沿x轴翻折，再向右平移3个单位₁B₁C₁ ，把这两步操作规定为翻移变换，如图，已知等边三角形ABC的顶点B（1，1），（3，1）．把△ABC经过连续3次翻移变换得到△A₃B₃C₃ ，则点A的对应点A₃的坐标是（）

A、（5，- $\sqrt{3}$ ） B、（8，1+ $\sqrt{3}$ ） C、（11，-1- $\sqrt{3}$ ） D、（14，1+ $\sqrt{3}$ ）

查看试题解析
5. 若点 $P (- 2 ， 3)$ 与点 $Q (a ， b)$ 关于 $x$ 轴对称，则 $a$ ， $b$ 的值分别是（）

A、 $- 2$ ， $3$ B、 $2$ ， $3$ C、 $- 2$ ， $- 3$ D、 $2$ ， $- 3$

查看试题解析
6. 在平面直角坐标系 $x O y$ 中，点 $A (2 ， 4 + m)$ 与点B $(m ， n)$ 关于y轴对称，则 $m + n$ 的值为（）

A、0 B、1 C、2 D、 $- 1$

查看试题解析
7. 已知点 $P (m - 1 ， n + 2)$ 与点 $Q (n - 4 ， 2 m + 1)$ 关于 $y$ 轴对称，则 $H (m ， n)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 在平面直角坐标系中，点 $P (- 3 ， - 5)$ 关于 $x$ 轴对称的点的坐标是（）

A、 $(3 ， - 5)$ B、 $(- 3 ， - 5)$ C、 $(3 ， 5)$ D、 $(- 3 ， 5)$

查看试题解析
9. 已知点 $Р (2 ， a)$ 与 $Q (2 ， b)$ 关于x轴对称，则 $a + b =$ （）

A、1 B、0 C、4 D、2

查看试题解析
10. 如图，在直角坐标系中， $△ A B C$ 各点坐标分别为 $A (- 2 ， 1)$ ， $B (- 1 ， 3)$ ， $C (- 4 ， 4)$ ．先作 $△ A B C$ 关于x轴成轴对称的 $△ A_{1} B_{1} C_{1}$ ，再把 $△ A_{1} B_{1} C_{1}$ 平移后得到 $△ A_{2} B_{2} C_{2}$ ．若 $B_{2} (2 ， 1)$ ，则点 $A_{2}$ 坐标为（）

A、 $(1 ， 5)$ B、 $(1 ， 3)$ C、 $(5 ， 3)$ D、 $(5 ， 5)$

查看试题解析

二、填空题

11. 在平面直角坐标系中， $A (- 1 ， 2)$ ， $B (m ， n)$ ，若 $A B ∥ x$ 轴， $A B = 3$ ，则 $m n =$ .

查看试题解析
12. 平面直角坐标系中，点 $P (3 ， - 2)$ 关于点 $Q (1 ， 0)$ 成中心对称的点的坐标是．

查看试题解析
13. 点 $M (- 4 ， 3)$ 关于x轴对称的点的坐标是．

查看试题解析
14. 若点 $A (2 ， a)$ 与点 $B (- 2 ， 5)$ 关于y轴对称，则a的值为 .

查看试题解析
15. 若点 $A （ - 5 ， m ）， B （ n ， 4 ）$ 关于y轴对称，则 $m + n$ 的值为.

查看试题解析

三、解答题

16. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）．

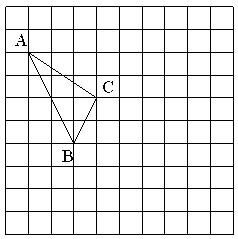
( 1 )请在如图所示的网格平面内作出平面直角坐标系；

( 2 )请作出△ABC关于y轴对称的△A′B′C′；

( 3 )写出点B′的坐标．

查看试题解析
17. $△ A B C$ 在平面直角坐标系中的位置如图所示，A、B、C三点在格点上，点B的坐标为 $(1 ， 1)$ ．

（ 1 ）作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

（ 2 ）作出 $△ A_{1} B_{1} C_{1}$ 关于y轴对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $A_{2}$ 的坐标，

查看试题解析
18. 如图，利用关于坐标轴对称的点的坐标的特点，画出与 $△ A B C$ 关于x轴对称的图形．

查看试题解析
19. 如图，利用关于坐标轴对称的点的坐标的特点，作出 $△$ ABC关于x轴对称的图形.

查看试题解析

四、综合题

20. 如图，在边长为1的小正方形所组成的网格上，每个小正方形的顶点都称为“格点”， $△ A B C$ 的顶点都在格点上，用直尺完成下列作图：

(1)、作出 $△ A B C$ 关于直线 $M N$ 的对称图形；

(2)、 $△ A B C$ 的面积为．

查看试题解析
21. 已知点 $A (3 x - 5 ， 6 - 2 x)$ ， B点坐标为 $(1 ， - 2)$ ．

(1)、若点A和点B关于x轴对称，求A点坐标；

(2)、若直线 $A B ∥ x$ 轴，求A点坐标．

查看试题解析
22. 点 $P (m + 3 ， 3 - 2 m)$ 与点 $Q (m^{2} - 5 m ， | 2 m - 3 |)$ 在同一平面直角坐标系中．

(1)、若点 $P$ 位于第四象限，求 $m$ 的取值范围；

(2)、若点 $P$ 与点 $Q$ 关于 $y$ 轴对称，求线段 $P Q$ 的长度．

查看试题解析
23. 如图所示，在平面直角坐标系中，已知 $A (2 ， 0)$ 、 $B (0 ， 3)$ 、 $C (3 ， 2)$ ；

(1)、若点 $P$ 与点 $C$ 关于 $x$ 轴对称，则点 $P$ 的坐标为；

(2)、在平面直角坐标系中画出 $△ A B C$ 关于 $y$ 轴对称的图形 $△ D E F$ ；

(3)、已知 $Q$ 为y轴上一点，若 $△ A B Q$ 的面积为2，直接写出点 $Q$ 的坐标.

查看试题解析

（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册 13.2 画轴对称图形同步分层训练（提升卷）