(人教版)2023-2024学年八年级数学上册 13.1 轴对称 同步分层训练(培优卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
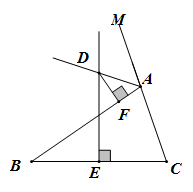
1. 如图,在R中,∠ABC=90°,以AC为边,作 , 满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE.下列结论中正确的有( )

①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE .
A、①②③ B、②③④ C、②③ D、①②④2. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .对于三人的答案,下列结论正确的是( )
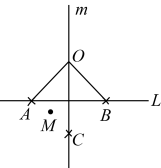 A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确3. 如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠MCB的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF﹣CG=CA;③DE=DC;④CF=2CD+EG;其中正确的有( )
A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确3. 如图,在Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠MCB的平分线CF相交于点D,AD交CB于点P,CF交AB的延长线于点F,过点D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长交FG于点H,则下列结论:①∠CDA=45°;②AF﹣CG=CA;③DE=DC;④CF=2CD+EG;其中正确的有( )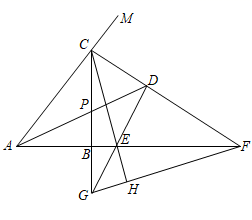 A、②③ B、②④ C、①②③④ D、①③④4. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P, ,PG AD交BC于F,交AB于G,① ;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )
A、②③ B、②④ C、①②③④ D、①③④4. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P, ,PG AD交BC于F,交AB于G,① ;②S△PAC:S△PAB=PC:PB;③BP垂直平分CE;④∠PCF=∠CPF.其中正确的有( )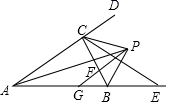 A、①②④ B、①③④ C、②③④ D、①③5. 如图,已知钝角中,且 , (1)以C为圆心,长为半径画弧;(2)以B为圆心,为半径画弧,交前弧于点E;(3)连接AE交的延长线于点D.下列叙述不一定正确的是( )
A、①②④ B、①③④ C、②③④ D、①③5. 如图,已知钝角中,且 , (1)以C为圆心,长为半径画弧;(2)以B为圆心,为半径画弧,交前弧于点E;(3)连接AE交的延长线于点D.下列叙述不一定正确的是( )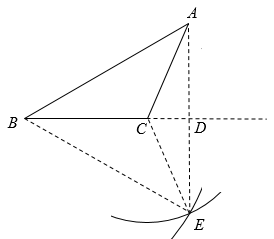 A、是等边三角形 B、平分 C、 D、BD垂直平分AE6. 如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )
A、是等边三角形 B、平分 C、 D、BD垂直平分AE6. 如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE,其中正确的是( )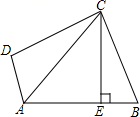 A、② B、①②③ C、①②④ D、①②③④7. 如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=62°,∠AEB=82°,则∠EBD的度数为( )
A、② B、①②③ C、①②④ D、①②③④7. 如图,线段AB,DE的垂直平分线交于点C,且∠ABC=∠EDC=62°,∠AEB=82°,则∠EBD的度数为( )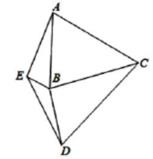 A、108° B、118° C、138° D、144°8. 如图, , ,这个图形叫做“筝形”,数学兴趣小组几名同学探究出关于它的如下结论:① ;② ;③ ;④ ;⑤“筝形”是轴对称图形.其中正确的结论有( )
A、108° B、118° C、138° D、144°8. 如图, , ,这个图形叫做“筝形”,数学兴趣小组几名同学探究出关于它的如下结论:① ;② ;③ ;④ ;⑤“筝形”是轴对称图形.其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个9. 如图,在四边形 ABCD 中,∠C=70°,∠B=∠D=90°,E、F 分别是 BC、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为( )
A、2个 B、3个 C、4个 D、5个9. 如图,在四边形 ABCD 中,∠C=70°,∠B=∠D=90°,E、F 分别是 BC、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为( )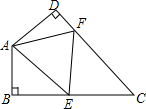 A、30° B、40° C、50° D、70°10. 如图, ,点B关于 的对称点E恰好落在 上,若 ,则 的度数为( )
A、30° B、40° C、50° D、70°10. 如图, ,点B关于 的对称点E恰好落在 上,若 ,则 的度数为( ) A、45° B、 C、 D、
A、45° B、 C、 D、二、填空题
-
11. 如图,在△ABC中,D为AB中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥BC交AC于点F,AC=8,BC=12,则BF的长为.
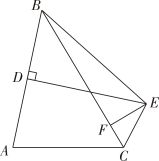 12. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
12. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度. 13. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
13. 如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .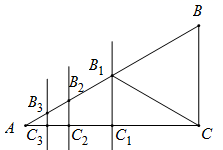 14. 如图,在△ABC中,∠BAC=124°,分别作AC,AB两边的垂直平分线PM,PN,垂足分别是点M,N.以下说法:①∠P=56°;②∠EAF=68°;③PE=PF;④点P到点B和点C的距离相等.正确的是(填序号).
14. 如图,在△ABC中,∠BAC=124°,分别作AC,AB两边的垂直平分线PM,PN,垂足分别是点M,N.以下说法:①∠P=56°;②∠EAF=68°;③PE=PF;④点P到点B和点C的距离相等.正确的是(填序号).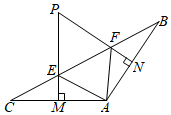 15. 如图,△ABC中(AB>BC),G在CB的延长线上,边AC的垂直平分线DE与∠ABG的角平分线交于点M,与AB交于点D,与AC相交于E,MN⊥AB于N.已知AB=13,BC=9,MN=3,则△BMN的面积是.
15. 如图,△ABC中(AB>BC),G在CB的延长线上,边AC的垂直平分线DE与∠ABG的角平分线交于点M,与AB交于点D,与AC相交于E,MN⊥AB于N.已知AB=13,BC=9,MN=3,则△BMN的面积是.
三、解答题
-
16. 如图,ABC的边BC的垂直平分线DE交ABC的外角平分线AD于点D,DF⊥AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.
 17. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
17. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF. 18. 如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
18. 如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.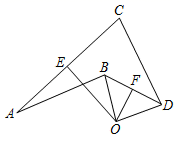 19.
19.如图,△ABC在平面直角坐标系中,其顶点坐标分别为A(-2,2),B(-4,-2),C(-1,-2).在坐标系中画出△ABC关于y轴对称的△A′B′C′.

四、综合题
-
20. 如图,将线段平移得到 , 使与对应,与对应,连接 , .
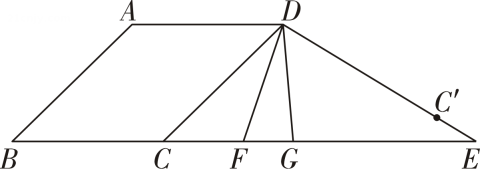 (1)、求证:;(2)、点在的延长线上,点与关于直线对称,直线交的延长线于点 . 点在线段上,且 .
(1)、求证:;(2)、点在的延长线上,点与关于直线对称,直线交的延长线于点 . 点在线段上,且 .①设 , 求的度数(用含的代数式表示);
②证明: .
21. 如图,在中,为的中点, , , 动点从点出发,沿方向以每秒的速度向点运动;同时动点从点出发,沿方向以每秒的速度向点A运动,运动时间是秒.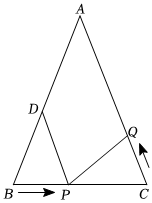 (1)、在运动过程中,当点位于线段的垂直平分线上时,求出的值;(2)、在运动过程中,是否存在某一时刻 , 使和全等,若存在,求出的值.若不存在,请说明理由.22. 如图,在中,是边上的高,为的角平分线,且 . 为的中线,延长到点 , 使得 , 连接 , 交于点 , 交于点 .
(1)、在运动过程中,当点位于线段的垂直平分线上时,求出的值;(2)、在运动过程中,是否存在某一时刻 , 使和全等,若存在,求出的值.若不存在,请说明理由.22. 如图,在中,是边上的高,为的角平分线,且 . 为的中线,延长到点 , 使得 , 连接 , 交于点 , 交于点 .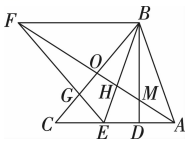 (1)、试说明;(2)、若 . 试判断与相等吗?为什么?23. 如图1,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.
(1)、试说明;(2)、若 . 试判断与相等吗?为什么?23. 如图1,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.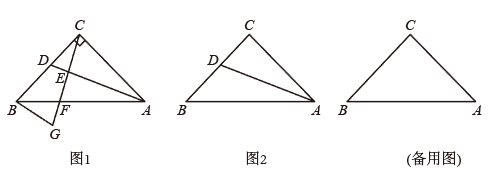 (1)、写出与BG相等的线段,并证明.(2)、若点D为线段BC的中点,其余条件不变,连接DF.根据题意,先在图2中补全图形,再证明:∠BDF=∠CDE.(3)、当点C和点F关于直线AD成轴对称时,直接写出线段CE,DE,AD三者之间的数量关系.
(1)、写出与BG相等的线段,并证明.(2)、若点D为线段BC的中点,其余条件不变,连接DF.根据题意,先在图2中补全图形,再证明:∠BDF=∠CDE.(3)、当点C和点F关于直线AD成轴对称时,直接写出线段CE,DE,AD三者之间的数量关系.