(人教版)2023-2024学年八年级数学上册 13.1 轴对称 同步分层训练(提升卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 如图,等腰中, , , AB的垂直平分线DE交AB于点D , 交AC于点E , 则的周长为( )
 A、12 B、8 C、15 D、132. 如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )
A、12 B、8 C、15 D、132. 如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )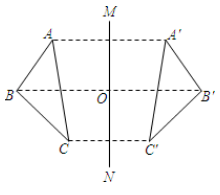 A、 B、 C、 D、3. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( )
A、 B、 C、 D、3. 如图,在中,是的垂直平分线,连接 . 以A为圆心,任意长为半径画弧,分别交于点E,F,分别以E,F为圆心,以大于长为半径画弧,两圆弧交于G点,作射线交于点H,则的度数为( ) A、36° B、25° C、24° D、21°4. 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应该挖在( )
A、36° B、25° C、24° D、21°4. 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应该挖在( ) A、三条角平分线的交点处 B、三条中垂线的交点处 C、三条高线所在直线的交点处 D、三条中线的交点处5. 如图,已知 , , 用尺规作图的方法在上取一点 , 使得 , 则下列选项正确的是( )
A、三条角平分线的交点处 B、三条中垂线的交点处 C、三条高线所在直线的交点处 D、三条中线的交点处5. 如图,已知 , , 用尺规作图的方法在上取一点 , 使得 , 则下列选项正确的是( ) A、
A、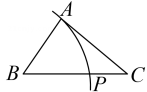 B、
B、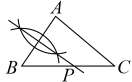 C、
C、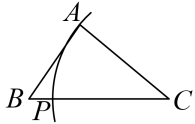 D、
D、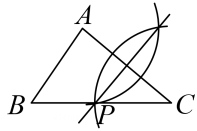 6. 如所示四个图案中,不是轴对称图形的是( )A、
6. 如所示四个图案中,不是轴对称图形的是( )A、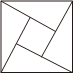 B、
B、 C、
C、 D、
D、 7. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( )
7. 如图,在中,分别以点和点为圆心,大于长为半径画弧,两弧相交于点 , 。作直线 , 交于点 , 交于点 , 连接。若 , , , 则的周长为( ) A、25 B、22 C、20 D、148. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( )
A、25 B、22 C、20 D、148. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若的周长为 , 则的周长为( ) A、 B、 C、 D、9. 如图,在中, , , 请观察尺规作图的痕迹( , , 分别是连线与边的交点),则的度数是( )
A、 B、 C、 D、9. 如图,在中, , , 请观察尺规作图的痕迹( , , 分别是连线与边的交点),则的度数是( ) A、 B、 C、 D、10. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
A、 B、 C、 D、10. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( ) A、10.5 B、12 C、15 D、18
A、10.5 B、12 C、15 D、18二、填空题
-
11. 如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F.若△AEF的周长为10cm ,则BC的长为 cm.
 12. 如图,的周长为20,AC的垂直平分线交BC于点 , 垂足为 , 若 , 则的周长是.
12. 如图,的周长为20,AC的垂直平分线交BC于点 , 垂足为 , 若 , 则的周长是. 13. 如图,中, , 点是上一点,、的垂直平分线分别交、于点、 , 则的度数为 .
13. 如图,中, , 点是上一点,、的垂直平分线分别交、于点、 , 则的度数为 .
 14. 如图,在中,分别以点和点为圆心,大于的长为半径作弧,两弧相交于点和点作直线交于点 , 连接若 , , 则的周长为 .
14. 如图,在中,分别以点和点为圆心,大于的长为半径作弧,两弧相交于点和点作直线交于点 , 连接若 , , 则的周长为 . 15. 如图,将一个长方形纸条折成如图所示的形状,若 , 则的度数 .
15. 如图,将一个长方形纸条折成如图所示的形状,若 , 则的度数 .

三、解答题
-
16. 如图,在△ABC中,AB=AC,∠B+∠C=60°,BC=15cm,ED、FG分别是AB、AC的垂直平分线,求GE的长.
 17. 如图,在△ABC中,AF平分∠BAC交BC于点F,AC的垂直平分线交BC于点E,交AC于点D,∠B=60°,∠C=26°,求∠FAE的度数.
17. 如图,在△ABC中,AF平分∠BAC交BC于点F,AC的垂直平分线交BC于点E,交AC于点D,∠B=60°,∠C=26°,求∠FAE的度数.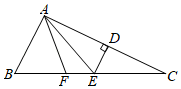 18. 如图,在中是的垂直平分线, , 的周长为 , 求的周长.
18. 如图,在中是的垂直平分线, , 的周长为 , 求的周长. 19. 如图,是五边形的一边,若垂直平分 , 垂足为M , 且 ▲ , ▲ , 则 ▲ .
19. 如图,是五边形的一边,若垂直平分 , 垂足为M , 且 ▲ , ▲ , 则 ▲ .给出下列信息:①平分;②;③ . 请从中选择适当信息,将对应的序号填到横线上方,使之构成真命题,补全图形,并加以证明.

四、综合题
-
20. 如图,已知中,垂直平分交于点 , 交于点 , 连接 .
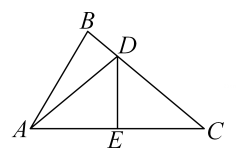 (1)、若 , , 求的度数;(2)、若 , , 求的周长.
(1)、若 , , 求的度数;(2)、若 , , 求的周长.