(人教版)2023-2024学年七年级数学上册 4.4 课题学习 设计制作长方体形状的包装纸盒 同步分层训练(培优卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 在正方体的表面上画有如图1中所示的粗线,图2是其展开图的示意图,但只在A面上画有粗线,那么将图1中剩余两个面中的粗线画入图2中,画法正确的是( )
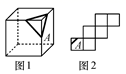 A、
A、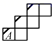 B、
B、 C、
C、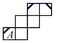 D、
D、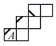 2. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .
2. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .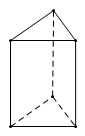 A、28 B、31 C、34 D、363. 有一种正方体如图所示,下列图形是该方体的展开图的是( )
A、28 B、31 C、34 D、363. 有一种正方体如图所示,下列图形是该方体的展开图的是( )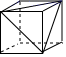 A、
A、 B、
B、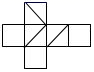 C、
C、 D、
D、 4. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
4. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )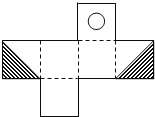 A、
A、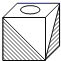 B、
B、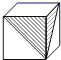 C、
C、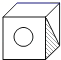 D、
D、 5. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )
5. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )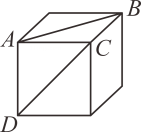 A、 B、 C、 D、6. 将坐标的正方体展开能得到的图形是( )
A、 B、 C、 D、6. 将坐标的正方体展开能得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,是一个正方体的平面展开图,且相对两个面表示的整式的和都相等,如果 ,则E所代表的整式是( )
7. 如图,是一个正方体的平面展开图,且相对两个面表示的整式的和都相等,如果 ,则E所代表的整式是( )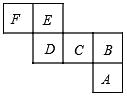 A、 B、 C、 D、8.
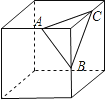
A、 B、 C、 D、8.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
 A、
A、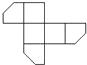
B、
B、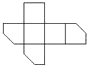
C、
C、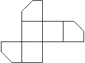
D、
D、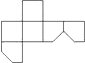
9. 如下图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和五边形,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图是( )
9. 如下图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和五边形,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图是( )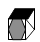 A、
A、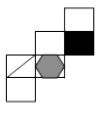 B、
B、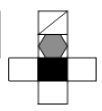 C、
C、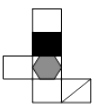 D、
D、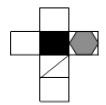 10. 如图所示的是某个正方体表面展开图的一种,折叠成正方体后,与“赞”字所在面相对面上的字是 ( )
10. 如图所示的是某个正方体表面展开图的一种,折叠成正方体后,与“赞”字所在面相对面上的字是 ( )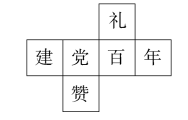 A、礼 B、年 C、百 D、建
A、礼 B、年 C、百 D、建二、填空题
-
11. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.12. 如图是一个正方体纸盒的展开图,正方体的各面标有数1,2,3,-3, , , 相对面上的两个数互为相反数,则 .
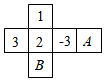 13. 如图:一个正方体的侧面展开图,相对的面是一对相反数,则.
13. 如图:一个正方体的侧面展开图,相对的面是一对相反数,则.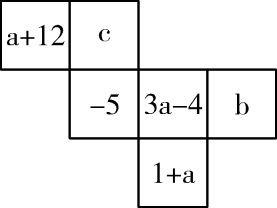 14. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .
14. 如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,a-b= .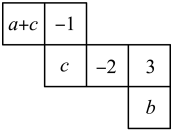 15. 仓库里有如图四种规格数量足够多的长方形、正方形的铁片尺寸单位:分米;从中选5块铁片,焊接成一个无盖的长方体或立方体铁盒不浪费材料甲型盒是由3种规格铁片焊接而成的表面积最大的铁盒,乙型盒是由2种规格铁片焊接而成的容积最小的铁盒.现在要分别做上述两种铁盒各100个,则至少需要号铁片块.
15. 仓库里有如图四种规格数量足够多的长方形、正方形的铁片尺寸单位:分米;从中选5块铁片,焊接成一个无盖的长方体或立方体铁盒不浪费材料甲型盒是由3种规格铁片焊接而成的表面积最大的铁盒,乙型盒是由2种规格铁片焊接而成的容积最小的铁盒.现在要分别做上述两种铁盒各100个,则至少需要号铁片块.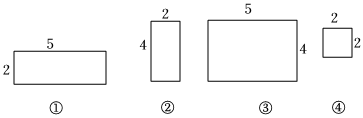
三、解答题
-
16. 如图所示的平面图分别是由哪种几何体展开形成的?
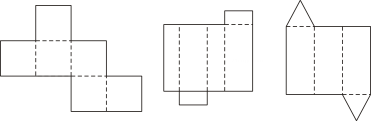
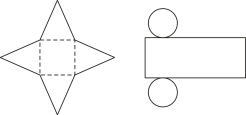
⑴ ▲ ;⑵ ▲ ;⑶ ▲ ;⑷ ▲ ;⑸ ▲ ;
17.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
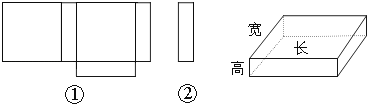
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
18.回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
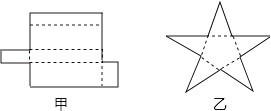
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
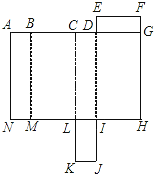
19.如图所示是长方体的表面展开图,折叠成一个长方体.
(1)与字母F重合的点有哪几个?
(2)若AD=4AB,AN=3AB,长方形DEFG的周长比长方形ABMN的周长少8,求原长方体的容积.
四、综合题
-
20. 如图,是一个几何体的表面展开图.
 (1)、该几何体是 .(2)、依据图中数据求该几何体的表面积和体积.21. 计算:(1)、先化简,再求值: , 其中 , ;(2)、如图是一个长方体纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)、该几何体是 .(2)、依据图中数据求该几何体的表面积和体积.21. 计算:(1)、先化简,再求值: , 其中 , ;(2)、如图是一个长方体纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数.
①填空:a= ▲ , b= ▲ ;
②利用①中结果,先化简,再求值: .
22. 阅读与思考请阅读下列材料,并完成相应的任务:包装盒的展开图:如图①是一个同学们熟悉的包装盒如图②是它的一种表面展开图,小明将图②画在如图③所示的的网格中.
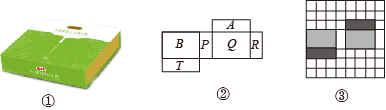 (1)、在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )A、字母B; B、字母A; C、字母R; D、字母T(2)、若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.
(1)、在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )A、字母B; B、字母A; C、字母R; D、字母T(2)、若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.五、实践探究题
-
23. 综合实践
问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
(1)、若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?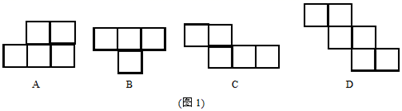 (2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
(2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?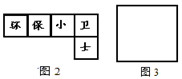 (3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
(3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高以及底面积,当小正方形边长为4cm时,求纸盒的容积.