安徽省合肥市三十八中新校2023-2024学年九年级上学期第一次月考数学试卷

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共40分）

1. 抛物线 $y = \frac{1}{2} (x + 1)^{2} - 3$ 的顶点坐标是（　　）

A、（1，3） B、（-1，-3） C、（1，-3） D、（-1，3）

查看试题解析
2. 已知函数 $y = - \frac{1}{2} x^{2} + x$ ，当函数值y随x的增大而增大时，x的取值范围是（　　）

A、x＜1 B、x＞1 C、 $x < - \frac{1}{2}$ D、 $x > - \frac{1}{2}$

查看试题解析
3. 将抛物线y＝-5x²+1向左平移1个单位，再向下平移2个单位，所得的抛物线为（　　）

A、y＝-5（x-1）²-1 B、y＝-5（x-1）²-2 C、y＝-5（x+1）²-1 D、y＝-5（x+1）²+3

查看试题解析
4. 下列对二次函数y＝-x²+2x的图象的描述，正确的是（　　）

A、不经过原点 B、对称轴是y轴 C、经过点（m+1，-m²+1） D、在对称轴右侧y随x的增大而增大

查看试题解析
5. 已知二次函数y=mx²+x﹣1的图象与x轴有两个交点，则m的取值范围是（）

A、m＞﹣ $\frac{1}{4}$ B、m≥﹣ $\frac{1}{4}$ C、m＞﹣ $\frac{1}{4}$ 且m≠0 D、m≥﹣ $\frac{1}{4}$ 且m≠0

查看试题解析
6. 下列函数中，y的值随x值的增大而减小的是（　　）

A、y＝x²+1 B、y＝-x²+1 C、y＝2x+1 D、y＝-2x+1

查看试题解析
7. 若函数y＝（m-3）x²-4x+2的图象与x轴只有一个交点，则m的值是（　　）

A、3或5 B、3 C、4 D、5

查看试题解析
8. 已知二次函数y＝a（x-h）²+k（a≠0）的图象与一次函数y＝mx+n（m≠0）的图象交于（x₁ ， y₁）和（x₂ ， y₂）两点，（　　）

A、若a＜0，m＜0，则x₁+x₂＞2h B、若a＞0，m＜0，则x₁+x₂＞2h C、若x₁+x₂＞2h，则a＞0，m＞0 D、若x₁+x₂＜2h，则a＞0，m＜0

查看试题解析
9. 若关于x的二次函数y＝x²-ax+1，当x≤-2时，y随着x的增大而减小，且关于x的分式方程 $\frac{1}{2 - x} = 2 + \frac{1 - a x}{x - 2}$ 有正数解，那么所有满足条件的整数a的值有（　　）

A、6个 B、5个 C、4个 D、3个

查看试题解析
10. 新定义：[a，b，c]为二次函数y＝ax²+bx+c（a≠0，a，b，c为实数）的“图象数”，如：y＝x²-2x+3的“图象数”为[1，-2，3]，若“图象数”是[m，2m+4，2m+4]的二次函数的图象与x轴只有一个交点，则m的值为（　　）

A、-2 B、 $\frac{1}{4}$ C、-2或2 D、2

查看试题解析

二、填空题（本大题共4小题，共20分）

11. 如图，抛物线y＝px²-q与直线y＝ax-b交于A（-2，m），B（4，n）两点，则不等式px²+q＞ax+b的解集是．

查看试题解析
12. 已知抛物线y＝x²-3x-2023与x轴的一个交点为（a，0），则代数式a²-3a-2024的值为．

查看试题解析
13. 某抛物线形隧道的最大高度为 $16$ 米，跨度为 $40$ 米，按如图所示的方式建立平面直角坐标系，它对应的表达式为．

查看试题解析
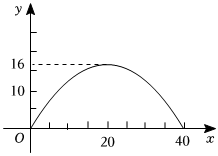14. 在平面直角坐标系中，关于x的函数y＝-x+3a+2和y＝x²-ax的图象相交于点P、Q．

(1)、若点P的横坐标为1，则a＝．

(2)、若P、Q两点都在x轴的上方，且a≠0，则实数a的取值范围是．

查看试题解析

三、计算题（本大题共1小题，共12分）

15. 某商店经营一种文具，已知成批购进时的单价是 $20$ 元．调查发现销售单价是 $30$ 元时，月销售量是 $230$ 件，而销售单价每上涨 $1$ 元，月销售量就减少 $10$ 件，且每件文具售价不能高于 $40$ 元，设每件文具的销售单价上涨了 $x$ 元时 $(x$ 为正整数 $)$ ，月销售利润为 $y$ 元．

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、每件文具的售价定为多少元时，月销售利润为 $2520$ 元？

(3)、每件文具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？

查看试题解析

四、解答题（本大题共8小题，共78分。）

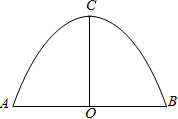
16. 已知抛物线的顶点坐标为（-1，-8），且过点（0，-6），求抛物线的解析式．

查看试题解析
17. 如图，这是一个横断面为抛物线形状的拱桥，此时水面宽 $A B$ 为 $3$ 米，拱桥最高点 $C$ 离水面的距离 $C O$ 也为 $3$ 米，则当水位上升 $2$ 米后，求水面的宽度．

查看试题解析
18. 已知函数y＝2x²-（3-k）x+k²-3k-10的图象经过原点，试确定k的值．

查看试题解析
19. 已知二次函数y＝x²+4x+k-1．

(1)、若抛物线与x轴有两个不同的交点，求k的取值范围；

(2)、若抛物线的顶点在x轴上，求k的值．

查看试题解析
20. 已知二次函数 $y = \frac{1}{2} x^{2} + x + 4$ ．

(1)、确定抛物线的开口方向、顶点坐标和对称轴方程；

(2)、当 $x$ 取何值时， $y$ 随 $x$ 的增大而增大？当 $x$ 取何值时， $y$ 随 $x$ 的增大而减小？

查看试题解析
21. 如图，在一面靠墙 $($ 墙足够长 $)$ 的空地上，用长为 $24$ 米的篱笆围成中间隔有二道篱笆的距形花圃，设花圃的一边 $A B$ 为 $x m$ ，面积为 $S m^{2}$ ．

(1)、求 $S$ 与 $x$ 的函数解析式及自变量 $x$ 的取值范围；

(2)、当 $x$ 取何值时，所围成的花圃面积最大？最大面积是多少？

查看试题解析
22. 如图所示，抛物线y＝ax²+bx+4（a≠0）经过点A（-1，0），点B（4，0），与y轴交于点C，连接AC，BC．点M是线段OB上不与点O、B重合的点，过点M作DM⊥x轴，交抛物线于点D，交BC于点E．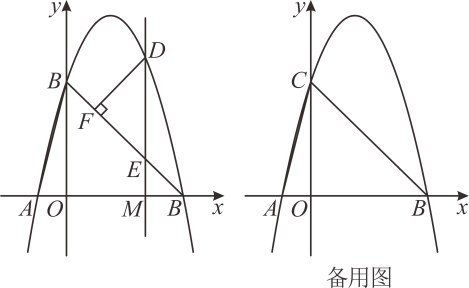

(1)、求抛物线的表达式；

(2)、过点D作DF⊥BC，垂足为点F．设M点的坐标为M（m，0），请用含m的代数式表示线段DF的长，并求出当m为何值时DF有最大值，最大值是多少？

查看试题解析
23. 已知抛物线y＝ax²-2x+1（a≠0）的对称轴为直线x＝1．

(1)、求a的值；

(2)、若点M（x₁ ， y₁），N（x₂ ， y₂）都在此抛物线上，且-1＜x₁＜0，1＜x₂＜2．比较y₁与y₂的大小，并说明理由；

(3)、设直线y＝m（m＞0）与抛物线y＝ax²-2x+1交于点A、B，与抛物线y＝3（x-1）²交于点C，D，求线段AB与线段CD的长度之比．

查看试题解析