(人教版)2023-2024学年七年级数学上册 4.3 角 同步分层训练(培优卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 如图,C,D在线段上,下列四个说法:
①直线上以B,C,D,E为端点的线段共有6条;
②图中有3对互为补角的角;
③若 , , 则以A为顶点的所有小于平角的角的度数和为370°;
④若 , , , 点F是线段上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为25
其中正确说法的个数是( )
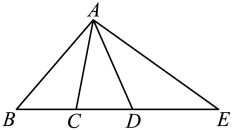 A、1个 B、2个 C、3个 D、4个2. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、3. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( )
A、1个 B、2个 C、3个 D、4个2. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、3. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( ) A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则4. 如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE=m°,∠EOF=90°,OM、ON分别平分∠AOE和∠BOF,下面说法:
A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则4. 如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE=m°,∠EOF=90°,OM、ON分别平分∠AOE和∠BOF,下面说法:①点E位于点O的北偏西m°;②图中互余的角有4对;③若∠BOF=4∠AOE,则∠DON=54°;④若 ,则n的倒数是 ,其中正确有( )
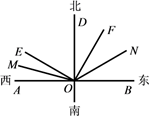 A、3个 B、2个 C、1个 D、0个5. 已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE= 则∠BOE的度数是( )
A、3个 B、2个 C、1个 D、0个5. 已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE= 则∠BOE的度数是( )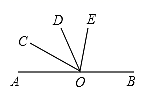 A、 B、 C、 D、6. 如图 ,垂足为D , ,下列结论正确的有( )
A、 B、 C、 D、6. 如图 ,垂足为D , ,下列结论正确的有( )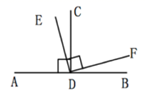
⑴ ;(2) ;(3) 与 互余;(4) 与 互补.
A、1个 B、2个 C、3个 D、4个7. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )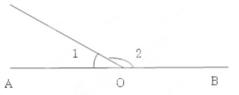 A、 B、 C、 D、∠2-∠18. 如图∠AOC=∠BOD= ,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:图中小于平角的角有6个;丙:∠AOB+∠COD = ;丁:∠BOC+∠AOD = .其中正确的结论有( ).
A、 B、 C、 D、∠2-∠18. 如图∠AOC=∠BOD= ,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:图中小于平角的角有6个;丙:∠AOB+∠COD = ;丁:∠BOC+∠AOD = .其中正确的结论有( ).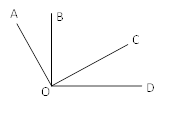 A、4个 B、3个 C、2个 D、1个9. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°10. 如图,已知O为直线AB上一点,OC平分 , , ,则 的度数为
A、4个 B、3个 C、2个 D、1个9. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°10. 如图,已知O为直线AB上一点,OC平分 , , ,则 的度数为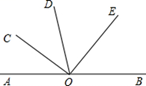 A、 B、
A、 B、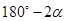 C、
C、 D、
D、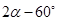
二、填空题
-
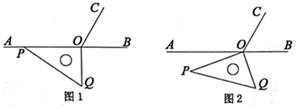
11. 如图1, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转(如图2所示),在旋转一周的过程中,第 秒时, 所在直线恰好平分 ,则 的值为.
 12. 小方同学设计了一个“魔法棒转不停”程序,如图所示,点 , 在直线 上,第一步, 绕点 顺时针旋转 度 至 ;第二步, 绕点 顺时针旋转 度至 ;第三步, 绕点 顺时针旋转 度至 , 以此类推,在旋转过程中若碰到直线 则立即绕点 反方向旋转.当 时,则 等于度.
12. 小方同学设计了一个“魔法棒转不停”程序,如图所示,点 , 在直线 上,第一步, 绕点 顺时针旋转 度 至 ;第二步, 绕点 顺时针旋转 度至 ;第三步, 绕点 顺时针旋转 度至 , 以此类推,在旋转过程中若碰到直线 则立即绕点 反方向旋转.当 时,则 等于度.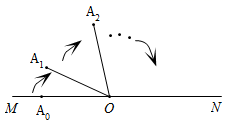 13. 已知在同一平面内,
13. 已知在同一平面内,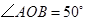 ,
,  ,则
,则 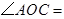 . 14. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)
. 14. 如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=70°,∠BOE= ∠BOC,∠BOD= ∠AOB,则∠DOE=°.(用含n的代数式表示)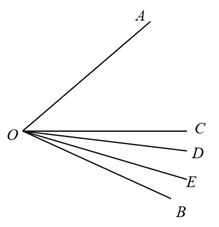 15. 我们将圆形钟面的时针和分针看作是两条从圆心发出的射线,当时针和分针夹角180度时形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“平衡时刻”,如图,6点整就是一个平衡时刻,请问从0时到24时共有个平衡时刻.
15. 我们将圆形钟面的时针和分针看作是两条从圆心发出的射线,当时针和分针夹角180度时形成一条直线,这条直线刚好平分钟面,我们将这样的时刻称为“平衡时刻”,如图,6点整就是一个平衡时刻,请问从0时到24时共有个平衡时刻.
三、解答题
-
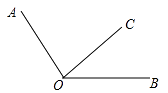
16. 如图,已知2∠BOC=∠AOC,∠AOC的余角比∠BOC小30°,作射线OD,使得∠AOC=4∠AOD,求∠DOB的度数.
 17. 地震后,许许多多志愿者到灾区投入了抗震救灾行列中.志愿者小方八点多准备前去为灾民服务,临出门他一看钟,时针与分针正好是重合的,下午两点多他拖着疲惫的身体回到家中,一进门看见钟的时针与分针方向相反,正好成一条直线,问小方是几点钟去为灾民服务?几点钟回到家?共用了多少时间?18. 如图,O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?
17. 地震后,许许多多志愿者到灾区投入了抗震救灾行列中.志愿者小方八点多准备前去为灾民服务,临出门他一看钟,时针与分针正好是重合的,下午两点多他拖着疲惫的身体回到家中,一进门看见钟的时针与分针方向相反,正好成一条直线,问小方是几点钟去为灾民服务?几点钟回到家?共用了多少时间?18. 如图,O是直线AB上一点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE互余的角有哪些?与∠DOE互补的角有哪些?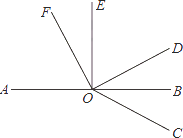 19. 已知 , 平分 ,求 的度数.
19. 已知 , 平分 ,求 的度数.四、综合题
-
20. 如图,已知 , 为锐角,平分 , 射线在内部.
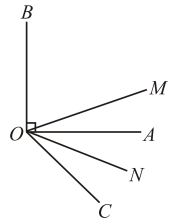 (1)、图中共有多少个小于平角的角?(2)、若 , , 求的度数.(3)、若 , , 请通过计算判断与的关系.21. 如图,∠AOB=90°,OM平分∠AOC,ON平分∠BOC.
(1)、图中共有多少个小于平角的角?(2)、若 , , 求的度数.(3)、若 , , 请通过计算判断与的关系.21. 如图,∠AOB=90°,OM平分∠AOC,ON平分∠BOC. (1)、若∠BOC=30°,求∠MON的度数;(2)、设∠BOC=(2x)°,能否求出∠MON的度数?若能,请求出其值;若不能,请说明理由;(3)、若将题干中“∠AOB=90°”改为“∠AOB=α(0°<α<90°)”,其他条件不变,设∠BOC=β,请用含α的式子表示∠MON的度数.22. 如图,已知同一平面内 , .
(1)、若∠BOC=30°,求∠MON的度数;(2)、设∠BOC=(2x)°,能否求出∠MON的度数?若能,请求出其值;若不能,请说明理由;(3)、若将题干中“∠AOB=90°”改为“∠AOB=α(0°<α<90°)”,其他条件不变,设∠BOC=β,请用含α的式子表示∠MON的度数.22. 如图,已知同一平面内 , .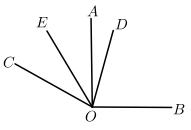 (1)、填空 .(2)、如平分 , 平分 , 直接写出的度数为°.(3)、试问在(2)的条件下,如果将题目中改成 , 其他条件不变,你能求出的度数吗?若能,请你写出求解过程;若不能,请说明理由.23. 如图,两条直线相交于点O,且 , 射线(与射线重合)绕点O逆时针方向旋转,速度为每秒 , 射线(与射线重合)绕点O顺时针方向旋转,速度为每秒 , 两射线 , 同时运动,运动时间为t秒(本题出现的角均指不大于平角的角).
(1)、填空 .(2)、如平分 , 平分 , 直接写出的度数为°.(3)、试问在(2)的条件下,如果将题目中改成 , 其他条件不变,你能求出的度数吗?若能,请你写出求解过程;若不能,请说明理由.23. 如图,两条直线相交于点O,且 , 射线(与射线重合)绕点O逆时针方向旋转,速度为每秒 , 射线(与射线重合)绕点O顺时针方向旋转,速度为每秒 , 两射线 , 同时运动,运动时间为t秒(本题出现的角均指不大于平角的角).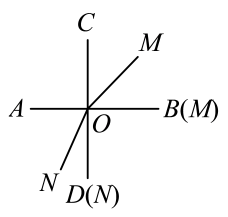 (1)、图中一定有个直角;当 , 的度数为;当 , 的度数为;(2)、当时,若 , 试求出t的值;(3)、当时,探究的值,在t满足怎样的条件时是定值,在t满足怎样的条件时不是定值?
(1)、图中一定有个直角;当 , 的度数为;当 , 的度数为;(2)、当时,若 , 试求出t的值;(3)、当时,探究的值,在t满足怎样的条件时是定值,在t满足怎样的条件时不是定值?