(人教版)2023-2024学年七年级数学上册 4.3 角 同步分层训练(提升卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 如图,将三个大小相同的正方形的一个顶点重合放置,则a,β,γ三个角的数量关系为( )
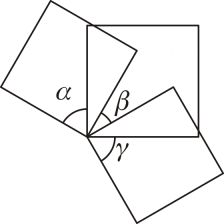 A、a+β+γ=90° B、a+β-γ=90° C、a-β+ γ= 90° D、a+2β-γ= 90°2. 一副三角尺按右上图所示位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果三角尺一边OB与90°刻度线重合,那么边OC与下列刻度线重合的是( )
A、a+β+γ=90° B、a+β-γ=90° C、a-β+ γ= 90° D、a+2β-γ= 90°2. 一副三角尺按右上图所示位置放置,OP为公共边,量角器中心与点O重合,OA为0°刻度线.如果三角尺一边OB与90°刻度线重合,那么边OC与下列刻度线重合的是( )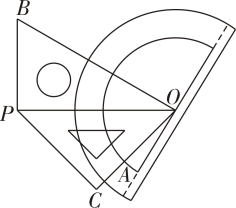 A、15°刻度线 B、30°刻 度线 C、45°刻度线 D、75°刻度线3. 如图,用同样大小的三角板比较∠A和∠B的大小,下列判断正确的是( )
A、15°刻度线 B、30°刻 度线 C、45°刻度线 D、75°刻度线3. 如图,用同样大小的三角板比较∠A和∠B的大小,下列判断正确的是( )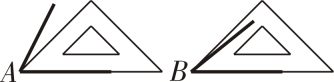 A、∠A>∠B B、∠A<∠B C、∠A=∠B D、没有量角器,无法确定4. 用“叠合法”比较∠1与∠2的大小,正确的是(A、
A、∠A>∠B B、∠A<∠B C、∠A=∠B D、没有量角器,无法确定4. 用“叠合法”比较∠1与∠2的大小,正确的是(A、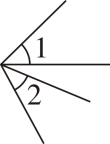 B、
B、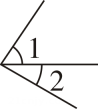 C、
C、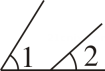 D、
D、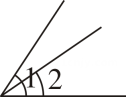 5. 在下图所示的4X4方格中,记∠ABD=α,∠DEF=β,∠CGH=γ,则( )
5. 在下图所示的4X4方格中,记∠ABD=α,∠DEF=β,∠CGH=γ,则( )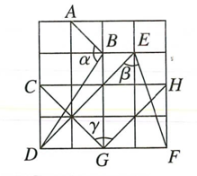 A、β≤a<γ B、β<y<a C、a<x<β D、a<β≤γ6. 下列换算中,错误的是( )A、47.28°=47°16'48” B、83.5°= 83°50' C、16°5'24"=16.09° D、0.25°= 900”7. 已知是的余角,且 , 则的补角等于( )A、 B、 C、 D、8. 如图,在同一平面内, , , 点为反向延长线上一点(图中所有角均指小于的角).下列结论:①;②;③;④.其中正确结论的个数有( ).
A、β≤a<γ B、β<y<a C、a<x<β D、a<β≤γ6. 下列换算中,错误的是( )A、47.28°=47°16'48” B、83.5°= 83°50' C、16°5'24"=16.09° D、0.25°= 900”7. 已知是的余角,且 , 则的补角等于( )A、 B、 C、 D、8. 如图,在同一平面内, , , 点为反向延长线上一点(图中所有角均指小于的角).下列结论:①;②;③;④.其中正确结论的个数有( ).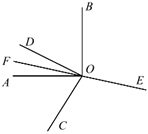 A、4个 B、3个 C、2个 D、1个9. 一副三角板如图摆放,则的度数是( )
A、4个 B、3个 C、2个 D、1个9. 一副三角板如图摆放,则的度数是( ) A、90° B、75° C、60° D、15°10. 如图,一张地图上有A、B、C三地,C地在A地的东南方向,若 , 则B地在A地的( )
A、90° B、75° C、60° D、15°10. 如图,一张地图上有A、B、C三地,C地在A地的东南方向,若 , 则B地在A地的( )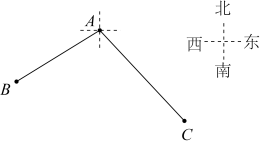 A、南偏西57°方向 B、南偏西67°方向 C、南偏西33°方向 D、西南方向
A、南偏西57°方向 B、南偏西67°方向 C、南偏西33°方向 D、西南方向二、填空题
-
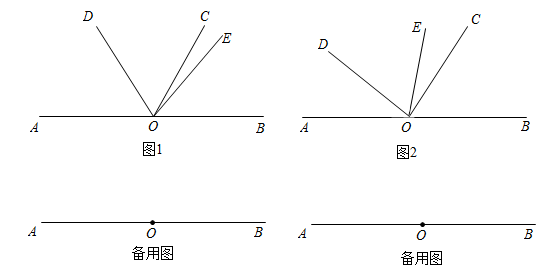
11. 若∠α=42°24',∠β=15.3°,则∠α与∠β的和等于12. 如图,在同一平面内,∠AOB=90°,∠AOC=25°,∠COD=50°,∠BOD>15°,则∠BOD的度数为
 13. 在同一平面内,若∠AOB=75°,∠AOC=27°,则∠BOC=14. 若∠A=25°12',∠B=25.12° ,则∠A与∠B的大小关系是∠A∠B. (用“<”“>”或“=”填空)15. 如图,小明在用量角器度量∠AOB的大小时,将边OB放在0刻度线上,但是顶点O放在中心点的右侧,此时边OA过50°刻度线,则∠AOB50°.(填“<”“=”或“> ”)
13. 在同一平面内,若∠AOB=75°,∠AOC=27°,则∠BOC=14. 若∠A=25°12',∠B=25.12° ,则∠A与∠B的大小关系是∠A∠B. (用“<”“>”或“=”填空)15. 如图,小明在用量角器度量∠AOB的大小时,将边OB放在0刻度线上,但是顶点O放在中心点的右侧,此时边OA过50°刻度线,则∠AOB50°.(填“<”“=”或“> ”)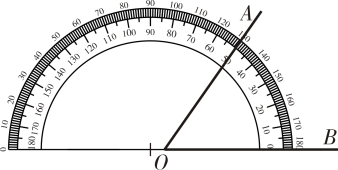
三、解答题
-
16. 已知一个角的余角比这个角补角的小12°,求这个角和它的余角的度数.17. 如图,一副直角三角板叠放在一起,若∠CAD=4∠BAD,请计算∠CAE的度数.
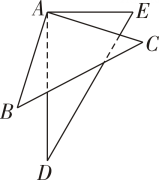 18. 如图,OD是∠BOC的平分线,OE是∠AOC的平分线,∠AOB︰∠BOC=3︰2,若∠BOE=13°,求∠DOE的度数.
18. 如图,OD是∠BOC的平分线,OE是∠AOC的平分线,∠AOB︰∠BOC=3︰2,若∠BOE=13°,求∠DOE的度数.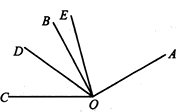 19. 如图,点O在直线上,已知 , 且射线平分 , , 求的度数.
19. 如图,点O在直线上,已知 , 且射线平分 , , 求的度数.
四、综合题
-
20. 如图,是直线,分别是的平分线.
 (1)、 , 求的度数.(2)、若 , 求.21. 如图,点A,O,B在同一条直线上, , , 分别是 , 的平分线.
(1)、 , 求的度数.(2)、若 , 求.21. 如图,点A,O,B在同一条直线上, , , 分别是 , 的平分线. (1)、若 , 求的度数;(2)、比较和的大小,并说明理由.
(1)、若 , 求的度数;(2)、比较和的大小,并说明理由.