(人教版)2023-2024学年七年级数学上册 4.2 直线、射线、线段 同步分层训练(培优卷)
试卷更新日期:2023-11-06 类型:同步测试
一、选择题
-
1. 在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段的长度为( )A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.52. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )
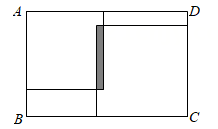 A、 B、 C、 D、3. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第二次将点A向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是( )
A、 B、 C、 D、3. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第二次将点A向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是( )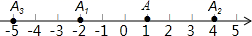 A、12 B、13 C、14 D、154. 已知A,B,C三点, , ,则 ( )A、8cm B、4cm C、8cm或4cm D、无法确定5. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A、12 B、13 C、14 D、154. 已知A,B,C三点, , ,则 ( )A、8cm B、4cm C、8cm或4cm D、无法确定5. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ) A、点A B、点B C、AB之间 D、BC之间6. 当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )A、﹣1≤x<6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1<x≤67. A、B、C中三个不同的点,则( )
A、点A B、点B C、AB之间 D、BC之间6. 当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )A、﹣1≤x<6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1<x≤67. A、B、C中三个不同的点,则( )
A、AB+BC=AC B、AB+BC>AC C、BC≥AB-AC D、BC=AB-AC8. 如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上,也可能在直线AB外9. 如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )A、4cm B、2cm C、4cm或2cm D、小于或等于4cm,且大于或等于2cm10. 点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )A、3 B、2 C、3或5 D、2或6二、填空题
-
11. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.

 12. 如图,数轴上O,A两点的距离为4,一动点P从点A出发,第1次跳动到的中点处,第2次从点 跳动到的中点处,第3次从点跳动到的中点处,按照这样的规律继续跳动到点 , , , …,处,那么线段的长度为 .
12. 如图,数轴上O,A两点的距离为4,一动点P从点A出发,第1次跳动到的中点处,第2次从点 跳动到的中点处,第3次从点跳动到的中点处,按照这样的规律继续跳动到点 , , , …,处,那么线段的长度为 .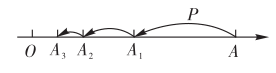 13. 同学们都知道,|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可以理解为5与﹣2两数在数轴上所对应的两点之间的距离,则使得|x﹣1|+|x+5|=6这样的整数x有个.14. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
13. 同学们都知道,|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可以理解为5与﹣2两数在数轴上所对应的两点之间的距离,则使得|x﹣1|+|x+5|=6这样的整数x有个.14. 如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)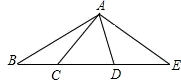 15. 如图,点 , 是直线 上的两点,点 , 在直线 上且点 在点 的左侧,点 在点 的右侧, , .若 ,则 .
15. 如图,点 , 是直线 上的两点,点 , 在直线 上且点 在点 的左侧,点 在点 的右侧, , .若 ,则 .
三、解答题
-
16. 如图,数轴上A点表示的数是﹣2,B点表示的数是5,C点表示的数是10.
 (1)、若要使A、C两点所表示的数是一对相反数,则“原点”表示的数是:.(2)、若此时恰有一只老鼠在B点,一只小猫在C点,老鼠发现小猫后立即以每秒一个单位的速度向点A方向逃跑,小猫随即以每秒两个单位的速度追击.
(1)、若要使A、C两点所表示的数是一对相反数,则“原点”表示的数是:.(2)、若此时恰有一只老鼠在B点,一只小猫在C点,老鼠发现小猫后立即以每秒一个单位的速度向点A方向逃跑,小猫随即以每秒两个单位的速度追击.①在小猫未抓住老鼠前,用时间t(秒)的代数式表示老鼠和小猫在移动过程中分别与点A之间的距离;
②小猫逮住老鼠时的“位置”恰好在 , 求时间t.17.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
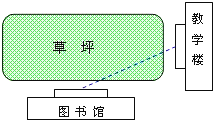
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
18.景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
 19. 结合数轴与绝对值的知识回答下列问题:
19. 结合数轴与绝对值的知识回答下列问题:数轴上表示和的两点之间的距离是 , 而;表示和两点之间的距离是 , 而;表示和两点之间的距离是 , 而 .
一般地,数轴上表示数和数的两点之间的距离公式为 .
 (1)、数轴上表示数的点与表示的点之间的距离为;(2)、数轴上表示数的点与表示的点之间的距离表示为 ;若数轴上位于与之间,求的值;(3)、如果表示数和的两点之间的距离是 , 则可记为: , 求的值.
(1)、数轴上表示数的点与表示的点之间的距离为;(2)、数轴上表示数的点与表示的点之间的距离表示为 ;若数轴上位于与之间,求的值;(3)、如果表示数和的两点之间的距离是 , 则可记为: , 求的值.四、综合题
-
20. 如图,已知数轴上 , 两点对应的数分别为 , , , 两点对应的数互为相反数.
 (1)、求 , 的长.(2)、若点从点出发,以每秒1个单位长度的速度向终点运动.当点到达点时,点从点出发,以每秒3个单位长度的速度向终点运动,设点的移动时间为(秒).
(1)、求 , 的长.(2)、若点从点出发,以每秒1个单位长度的速度向终点运动.当点到达点时,点从点出发,以每秒3个单位长度的速度向终点运动,设点的移动时间为(秒).①问为何值时,为的中点?
②当时,求的值.
21. 如图,在数轴上有A, , 三点,A,两点所对应的数分别是 , , 且满足是最大的负整数,是绝对值最小的有理数,点在点A的右侧,到点A的距离是个单位长度.请你解答下列问题: (1)、点A表示的数是 , 点表示的数是 , 点表示的数是;(2)、点 , 为数轴上两个动点,点从A点出发速度为每秒个单位长度,点 从点出发速度为每秒个单位长度,若 , 两点同时出发,相向而行,运动时间为秒.求当为何值时,点与点之间的距离是个单位长度?22. 如图,在数轴上有三个点 , , , 是原点,满足个单位长度.动点从点出发沿数轴向右以每秒2个单位长度的速度匀速运动;同时动点Q从点出发沿数轴向左匀速运动,速度为单位长度/秒.设点的运动时间为秒.
(1)、点A表示的数是 , 点表示的数是 , 点表示的数是;(2)、点 , 为数轴上两个动点,点从A点出发速度为每秒个单位长度,点 从点出发速度为每秒个单位长度,若 , 两点同时出发,相向而行,运动时间为秒.求当为何值时,点与点之间的距离是个单位长度?22. 如图,在数轴上有三个点 , , , 是原点,满足个单位长度.动点从点出发沿数轴向右以每秒2个单位长度的速度匀速运动;同时动点Q从点出发沿数轴向左匀速运动,速度为单位长度/秒.设点的运动时间为秒. (1)、当点运动到点时,;(2)、若 , 当点和点相遇时,;(3)、若 , 当 , 两点距离为16个单位长度时,求的值.23. 如图,点C在线段AB上, , 点D、E分别是AB和CB的中点, , .
(1)、当点运动到点时,;(2)、若 , 当点和点相遇时,;(3)、若 , 当 , 两点距离为16个单位长度时,求的值.23. 如图,点C在线段AB上, , 点D、E分别是AB和CB的中点, , .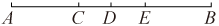 (1)、求线段CD,DE,AB的长;(2)、是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?(3)、是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?
(1)、求线段CD,DE,AB的长;(2)、是否存在点M,使它到A,C两点的距离之和等于8cm,为什么?(3)、是否存在点M,使它到A,C两点的距离之和大于10cm?如果点M存在,点M的位置应该在哪里?为什么?这样的点M有多少个?