（人教版）2023-2024学年七年级数学上册 4.2 直线、射线、线段同步分层训练（提升卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 数轴上的点A到原点的距离是2，则点A表示的数为（　　）

A、2 B、-2 C、1或-1 D、2或-2

查看试题解析
2. 如图1，在数轴上，点 $A$ 、 $B$ 分别表示 $a$ 、 $b$ ，且 $a + b = 0$ .若 $A$ 、 $B$ 两点之间的距离为6，则点 $A$ 表示的数为（）
图1

A、 $- 3$ B、0 C、3 D、 $- 6$

查看试题解析
3. 如图所示图形中，共有（）条线段．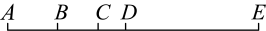

A、10 B、12 C、15 D、30

查看试题解析
4. 已知点 $A ， B ， C$ 在同一条直线上，且线段 $A B = 5$ ， $B C = 6$ ，则 $A ， C$ 两点间的距离是（）

A、 $1$ B、 $11$ C、 $1$ 或 $11$ D、 $3$ 或 $10$

查看试题解析
5. 在数轴上，把表示2的点沿着数轴移动7个单位长度得到的点所表示的数是（）

A、 $- 5$ B、9 C、 $\pm 9$ D、 $- 5$ 或9

查看试题解析
6. 如图，未标出原点的数轴上有 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 六个点，若相邻两点之间的距离相等，则点 $C$ 所表示的数是（）

A、7 B、10 C、13 D、15

查看试题解析
7. 已知点M在数轴上表示的数是－4，点N与点M的距离是3，则点N表示的数是（）

A、－1 B、－7 C、－1或－7 D、－1或1

查看试题解析
8. 已知数轴上点 $A$ 代表的数是3，点 $B$ 到原点的距离分别是9，则 $A$ ， $B$ 两点间的距离是（）

A、6 B、9或12 C、12 D、6或12

查看试题解析
9. 下列四个图中，能表示线段x=a+c-b的是（）

A、 B、 C、 D、

查看试题解析
10. 如果线段AB=10 cm，MA+ MB=13 cm，那么下面说法中正确的是（）

A、点M在线段AB上 B、点M在直线AB上 C、点M可能在直线AB上也可能在AB外 D、点M在直线AB外

查看试题解析

二、填空题

11. 点A为数轴上表示-2的动点，当点A沿数轴移动4个单位长到B时，点B所表示的数是．

查看试题解析
12. 与-3相距6个单位长度的数是。

查看试题解析
13. 下列图示中，直线表示方法正确的有（填序号）

查看试题解析
14. 若数轴上的点A和点B之间的距离为3个单位长度，已知点B表示的数是 $- 2$ ，则点A表示的数为．

查看试题解析
15. 已知线段AB＝7cm，在直线AB上画线段BC ，使它等于3cm，则线段AC＝cm．

查看试题解析

三、解答题

16. 如图，数轴上有四个点 $A$ ， $B$ ， $C$ ， $D$ ，相邻两点之间的距离均为 $m$ （ $m$ 为正整数），点 $B$ 表示的数为 $- 6$ ，设这四个点表示的数的和为 $n$ .

(1)、若 $m = 3$ ，则表示原点的是点，点 $A$ 表示的数是；

(2)、若点 $D$ 表示的数是32.
①求 $m$ 的值；
②直接写出 $n$ 的值.

查看试题解析
17. 根据如图给出的数轴，解答下面的问题：

(1)、观察数轴，与点A的距离为5个单位长度的点表示的数是：

(2)、已知点C到A、B两点距离和为10，求点C表示的数。

查看试题解析
18. 结合数轴与绝对值的知识回答下列问题：

(1)、数轴上表示4和1的两点之间的距离是；表示 $- 3$ 和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于 $| m - n |$ ．如果表示数a和 $- 2$ 的两点之间的距离是3，那么a＝；

(2)、若数轴上表示数a的点位于 $- 4$ 与2之间，求 $| a + 4 | + | a - 2 |$ 的值．

查看试题解析
19. 如图，已知线段AB=12，BC=4．

(1)、AC=

(2)、若P是线段AB延长线上任意一点，则PA+PB-2PC的值发生变化吗？若不变，值为多少？

查看试题解析

四、综合题

20. 如图，点O为数轴原点，点A对应的数为-5，点B对应的数为10.

(1)、点C是数轴上A、B之间的一个点，且 $4 C A = C B$ ，求线段CA的长及点C对应的数.

(2)、点P从点A出发以每秒2个单位的速度沿数轴正方向运动，点Q从点B出发以每秒1个单位的速度沿数轴负方向运动.P、Q两点同时出发，设运动时间为t秒.当满足 $A P + B Q = 2 P Q$ ，求运动时间t.

查看试题解析
21. 如图，已知直线 $A B$ ，射线 $A C$ ，线段 $B C$ .

(1)、用无刻度的直尺和圆规作图：延长 $B C$ 到点D，使 $C D = A C$ ，连接 $A D$ .

(2)、比较 $A B + A D$ 与 $B C + A C$ 的大小，并说明理由.

查看试题解析
22. 同学们，我们都知道： $| 5 - 2 |$ 表示 $5$ 与 $2$ 的差的绝对值，实际上也可理解为 $5$ 与 $2$ 两数在数轴上所对应的两点之间的距离； $| 5 + 2 |$ 表示 $5$ 与 $- 2$ 的差的绝对值，实际上也可理解为 $5$ 与 $- 2$ 两数在数轴上所对应的两点之间的距离，试探索：

(1)、 $| - 4 + 6 | =$ （）； $| - 2 - 4 | =$ （）；

(2)、写出使得 $| x + 2 | + | x - 1 | = 3$ 成立的所有整数；

(3)、若数轴上表示数a的点位于 $- 4$ 与 $6$ 之间，求 $| a + 4 | + | a - 6 |$ 的值.

查看试题解析
23. 数轴是学习有理数的一种重要工具，任何有理数都可以在数轴上表示，这样能够运用数形结合的方法解决一些问题，例如，两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示，如，在数轴上，有理数3与1对应的两点之间的距离为 $| 3 － 1 |$ =2，有理数5与-2对应的两点之间的距离为 $| 5 －（ - 2 ） |$ =7，有理数-8与-5对应的两点之间的距离为 $| - 8 －（ - 5 ） |$ =3.
如图，在数轴上有理数a对应的点为点A，有理数b对应的点为B，A，B两点之间的距离表示为 $| a － b |$ 或 $| b － a |$ ，记为 $| A B |$ = $| a － b |$ = $| b － a |$ .

(1)、解决问题：
数轴上有理数-10与3对应的两点之间的距离等于 ▲ ；数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为 ▲ ；若数轴上有理数x与1对应的两点A，B之间的距离 $| A B |$ =6，则x等于 ▲ .

(2)、联系拓广：
如图，点M，N，P是数轴上的三点，点M表示的数为4，点N表示的数为-2，动点P表示的数为x.
①若点P在点M，N两点之间，则 $| P M |$ + $| P N |$ = ▲ ；若 $| P M |$ + $| P N |$ =10，则点P表示的数x为 ▲ ；由此可得：当 $| x + 3 |$ + $| x － 7 |$ 取最小值时，整数x的所有取值的和为 ▲ .
②当点P到点M的距离等于点P到点N的距离的2倍时，请直接写出x的值.

查看试题解析

（人教版）2023-2024学年七年级数学上册 4.2 直线、射线、线段 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册 4.2 直线、射线、线段同步分层训练（提升卷）