北京市某中学2023-2024学年九年级上学期第二次调研数学试卷
试卷更新日期:2023-11-06 类型:月考试卷
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 中秋节是中国的传统节日,有“团圆”、“丰收”的寓意.月饼是首选传统食品,不仅美味,而且设计多样.下列月饼图案中,为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线的顶点坐标是( )A、 B、 C、 D、3. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、4. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
2. 抛物线的顶点坐标是( )A、 B、 C、 D、3. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、4. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( ) A、20° B、40° C、80° D、70°5. 如图是甲、乙两名同学五次数学测试成绩的折线图比较甲、乙两名同学的成绩,下列说法正确的是( )
A、20° B、40° C、80° D、70°5. 如图是甲、乙两名同学五次数学测试成绩的折线图比较甲、乙两名同学的成绩,下列说法正确的是( )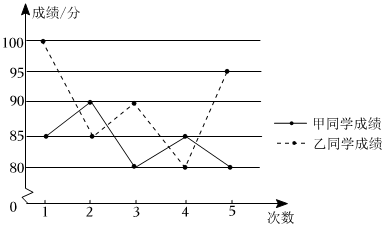 A、甲同学平均分高,成绩波动较小 B、甲同学平均分高,成绩波动较大
A、甲同学平均分高,成绩波动较小 B、甲同学平均分高,成绩波动较大
C、乙同学平均分高,成绩波动较小 D、乙同学平均分高,成绩波动较大6. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、97. 如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )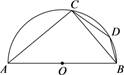 A、 B、 C、 D、8. 如图,线段 , 动点以每秒个单位长度的速度从点出发,沿线段运动至点以点为圆心,线段的长为半径作圆.设点的运动时间为 , 点 , 之间的距离为 , 的面积为则与 , 与满足的函数关系分别是( )
A、 B、 C、 D、8. 如图,线段 , 动点以每秒个单位长度的速度从点出发,沿线段运动至点以点为圆心,线段的长为半径作圆.设点的运动时间为 , 点 , 之间的距离为 , 的面积为则与 , 与满足的函数关系分别是( ) A、正比例函数关系、一次函数关系 B、一次函数关系,正比例函数关系
A、正比例函数关系、一次函数关系 B、一次函数关系,正比例函数关系
C、一次函数关系,二次函数关系 D、正比例函数关系,二次函数关系二、填空题(本大题共9小题,共21.0分)
-
9. 若点与点关于原点对称,则点坐标为 .10. 已知、是一次函数的图象上的两点,则 填“”或“”或“=”11. 将抛物线向下平移个单位长度,得到的抛物线是 .12. 如图,是的直径,是的切线,为切点,与交于点 , 连接若 , 则的度数为 .
 13. 某学校有一个矩形小花园,花园长米,宽米,现要在花园中修建人行雨道,如图所示,阴影部分为雨道,其余部分种植花卉,同样宽度的雨道有条,其中两条与矩形的宽平行,另外一条与矩形的宽垂直,计划花卉种植面积共为平方米,设雨道的宽为米,根据题意可列方程为 .
13. 某学校有一个矩形小花园,花园长米,宽米,现要在花园中修建人行雨道,如图所示,阴影部分为雨道,其余部分种植花卉,同样宽度的雨道有条,其中两条与矩形的宽平行,另外一条与矩形的宽垂直,计划花卉种植面积共为平方米,设雨道的宽为米,根据题意可列方程为 . 14. 如图, , 是的两条切线,切点分别为 , , 连接 , , 若 , 则
14. 如图, , 是的两条切线,切点分别为 , , 连接 , , 若 , 则 15. 如图,菱形的对角线交于点 , 点为的中点,连接若 , , 则的长为 .
15. 如图,菱形的对角线交于点 , 点为的中点,连接若 , , 则的长为 . 16. 学校组织学生参加木艺艺术品加工劳动实践活动.已知某木艺艺术品加工完成共需A,B,C,D,E,F,G七道工序,加工要求如下:
16. 学校组织学生参加木艺艺术品加工劳动实践活动.已知某木艺艺术品加工完成共需A,B,C,D,E,F,G七道工序,加工要求如下:①工序C,D须在工序A完成后进行,工序E须在工序B,D都完成后进行,工序F须在工序C,D都完成后进行;
②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;
③各道工序所需时间如下表所示:
工序
A
B
C
D
E
F
G
所需时间/分钟
9
9
7
9
7
10
2
在不考虑其他因素的前提下,若由一名学生单独完成此木艺艺术品的加工,则需要分钟;若由两名学生合作完成此木艺艺术品的加工,则最少需要分钟.
17. 解方程: .三、解答题(本大题共11小题,共63.0分。解答应写出文字说明,证明过程或演算步骤)
-
18.
已知:如图,点和 .
求作:直线 , 使得与相切于点 .
作法:①连接 , 分别以点和点为圆心,大于的长为半径作弧,两弧交于 , 两点;
②作直线 , 交于点;
③以点为圆心,以长为半径作 , 与相交,其中一个交点为点;
④作直线 .
直线即为所求作. (1)、使用直尺和圆规,依作法补全图形保留作图痕迹;
(1)、使用直尺和圆规,依作法补全图形保留作图痕迹;
(2)、完成下面的证明.
证明:由作法可知,点为线段的中点连接 .
为的直径,
填推理的依据 .
.
点在上,
是的切线 填推理的依据 .19. 已知关于x的一元二次方程 .(1)、求证:该方程总有两个不相等的实数根;(2)、若该方程的两个根均为负数,求a的取值范围.20.
如图,在平面直角坐标系中,的顶点坐标分别为 , , , 将绕点顺时针旋转得到 , 点旋转后的对应点为 .(1)、画出旋转后的图形 , 并写出点的坐标;
(2)、求出的面积. 21.
21.
如图,在中, , , 分别是 , 的中点, , . (1)、连接 , 若 , , 求的长.
(1)、连接 , 若 , , 求的长. (2)、求证:四边形是菱形;22.
(2)、求证:四边形是菱形;22.
在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点 .(1)、求这个一次函数的解析式;
(2)、当时,对于的每一个值,一次函数的值小于函数的值,直接写出的取值范围.23.
如图在中, , 是的角平分线,点在上,以点为圆心,长为半径的圆经过点 , 交于点 , 交于点 .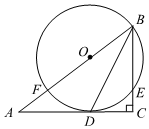 (1)、求证:是的切线;(2)、若 , , 求半径的长.24. 某公园内人工喷泉有一个竖直的喷水枪,喷出的水流路径可以看作是抛物线的一部分.记喷出的水流距喷水枪的水平距离为 , 距地面的竖直高度为 , 获得数据如表:
(1)、求证:是的切线;(2)、若 , , 求半径的长.24. 某公园内人工喷泉有一个竖直的喷水枪,喷出的水流路径可以看作是抛物线的一部分.记喷出的水流距喷水枪的水平距离为 , 距地面的竖直高度为 , 获得数据如表:小景根据学习函数的经验,对函数随自变量的变化而变化的规律进行了探究.
下面是小景的探究过程,请补充完整:(1)、在平面直角坐标系中,描出以表中各对对应值为坐标的点,并画出该函数的图象;
(2)、水流的最高点距喷水枪的水平距离为;
(3)、结合函数图象,解决问题:
公园准备在距喷水枪水平距离为处加装一个石柱,使该喷水枪喷出的水流刚好落在石柱顶端,则石柱的高度约为 25. 某校开展了“学习二十大”的知识竞赛百分制 , 七、八年级学生参加了本次活动为了解两个年级的答题情况,该校从每个年级各随机抽取了名学生的成绩,并对数据成绩进行了整理、描述和分析下面给出了部分信息.
25. 某校开展了“学习二十大”的知识竞赛百分制 , 七、八年级学生参加了本次活动为了解两个年级的答题情况,该校从每个年级各随机抽取了名学生的成绩,并对数据成绩进行了整理、描述和分析下面给出了部分信息.
七年级成绩的频数分布直方图如下
数据分成五组: , , , , :
, 七年级成绩在的数据如下单位:分:
七、八年级各抽取的名学生成绩的平均数、中位数、众数、方差如表:年级
平均数
中位数
众数
方差
七年级
八年级
根据以上信息,回答下列问题:
(1)、表中 , ;
(2)、下列推断合理的是 ;
样本中两个年级数据的平均数相同,八年级数据的方差较小,由此可以推断该校八年级学生成绩的波动程度较小;
若八年级小明同学的成绩是分,可以推断他的成绩超过了该校八年级一半以上学生的成绩.
(3)、竞赛成绩分及以上记为优秀,该校七年级有名学生,估计七年级成绩优秀的学生人数.26. 在平面直角坐标系xOy中,已知抛物线 .(1)、求该抛物线的对称轴(用含a的式子表示)(2)、 , 为该抛物线上的两点,若 , , 且 , 求a的取值范围.27. 如图,在等边三角形中,点为内一点,连接 , , , 将线段绕点顺时针旋转得到 , 连接 , .(1)、用等式表示与的数量关系,并证明;
(2)、当时,直接写出的度数为;
(3)、若为的中点,连接 , 用等式表示与的数量关系,并证明. 28.
28.
在平面直角坐标系中,图形上任意两点间的距离若有最大值,将这个最大值记为对于点和图形给出如下定义:点是图形上任意一点,若 , 两点间的距离有最小值,且最小值恰好为 , 则称点为图形的“关联点”(1)、如图 , 图形是矩形 , 其中点的坐标为 , 点的坐标为 , 则 ,在点 , , , 中,矩形的“关联点”是 . (2)、如图 , 图形是中心在原点的正方形 , 其中点的坐标为若直线上存在点 , 使点为正方形的“关联点”求的取值范围;
(2)、如图 , 图形是中心在原点的正方形 , 其中点的坐标为若直线上存在点 , 使点为正方形的“关联点”求的取值范围;
(3)、已知点 , 图形是以为圆心,为半径的若线段上存在点 , 使点为的“关联点“,直接写出的取值范围.