北京市朝阳区重点中学2023-2024学年九年级上学期调研数学试卷（9月份）

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8小题，共16.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列方程中是一元二次方程的是（）

A、 $x y + 2 = 1$ B、 $\frac{1}{x^{2}} - x = 1$ C、 $x (x - 3) = 0$ D、 $x^{3} + 2 x = 0$

查看试题解析
2. 用配方法解一元二次方程 $x^{2} - 8 x + 2 = 0$ ，此方程可化为的正确形式是（）

A、 ${(x - 4)}^{2} = 14$ B、 ${(x - 4)}^{2} = 18$ C、 ${(x + 4)}^{2} = 14$ D、 ${(x + 4)}^{2} = 18$

查看试题解析
3. 二次函数y=x²的图象经过的象限是（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
4. 对于 $y = 3 (x - 1)^{2} + 2$ 的性质，下列叙述正确的是（）

A、顶点坐标为 $(- 1 ， 2)$ B、当x>时， $y$ 随 $x$ 增大而减小 C、当 $x = 1$ 时， $y$ 有最大值 $2$ D、对称轴为直线 $x = 1$

查看试题解析
5. 一元二次方程 $4 x^{2} + 1 = - 4 x$ 的根的情况是（）

A、只有一个实数根 B、有两个不相等的实数根
C、有两个相等的实数根 D、没有实数根

查看试题解析
6. 已知 $x_{1}$ 和 $x_{2}$ 是方程 $x^{2} - x - 1 = 0$ 的两个根，则 $x_{1}^{2} + x_{1} x_{2} + x_{2}^{2}$ 的值是（）

A、 $1$ B、 $2$ C、 $3$ D、 $- 1$

查看试题解析
7. 已知点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 是抛物线 $y = (x - 1)^{2} - 2$ 上两点，若 $x_{1} < x_{2} < 0$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} = y_{2}$ D、以上都有可能

查看试题解析
8. 如图，在平面直角坐标系 $x O y$ 中，有五个点 $A (2 ， 0)$ ， $B (0 ， - 2)$ ， $C (- 2 ， 4)$ ， $D (4 ， - 2)$ ， $E (7 ， 0)$ ，将二次函数 $y = a (x - 2)^{2} + m (m \neq 0)$ 的图象记为 $W .$ 下列判断中：
$① A$ 一定不在 $W$ 上；
$②$ 点 $B$ ， $C$ ， $D$ 可以同时在 $W$ 上；
$③$ 点 $C$ ， $E$ 不可能同时在 $W$ 上．
所有正确结论的序号是（）

A、 $① ② ③$ B、 $① ②$ C、 $① ③$ D、 $② ③$

查看试题解析

二、填空题（本大题共8小题，共16.0分）

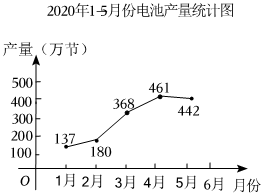
9. 请写出一个开口向下，对称轴为直线 $x = 3$ 的抛物线的解析式．

查看试题解析
10. 若关于 $x$ 的一元二次方程 $(a - 1) x^{2} + a^{2} x - a = 0$ 有一个根是 $x = 1$ ，则 $a$ 的值为．

查看试题解析
11. 某厂家 $2020$ 年 $1 ～ 5$ 月份的口罩产量统计如图所示，设从2月份到3月份，该厂家口罩产量的月平均增长率为 $x$ ，根据题意可得方程．

查看试题解析
12. 正方形边长为2，若边长增加x，那么面积增加y，则y与x的函数关系式是．

查看试题解析
13. 将抛物线 $y = 3 x^{2}$ 向右平移 $1$ 个单位，再向上平移 $2$ 个单位后所得到的抛物线的解析式为．

查看试题解析
14. $a$ 是关于 $x$ 的一元二次方程 $x^{2} + 2 x - 5 = 0$ 的根，则 $2 a^{2} + 4 a - 1$ 的值是．

查看试题解析
15. 李伟同学在解关于 $x$ 的一元二次方程 $x^{2} - 3 x + m = 0$ 时，误将 $- 3 x$ 看作 $+ 3 x$ ，结果解得 $x_{1} = - 1$ ， $x_{2} = - 2$ ，则原方程的解为．

查看试题解析
16. 一个 $33$ 人的旅游团到一家酒店住宿，酒店的客房只剩下 $4$ 间一人间和若干间三人间，住宿价格是一人间每晚 $100$ 元，三人间每晚 $130$ 元 $. ($ 说明：男士只能与男士同住，女士只能与女士同住，三人间客房可以不住满，但每间每晚仍需支付 $130$ 元 $.)$
$(1)$ 若该旅游团一晚的住宿房费为 $1530$ 元，则他们租住了间一人间；
$(2)$ 若该旅游团租住了 $3$ 间一人间，且共有 $19$ 名男士，则租住一晚的住宿房费最少为元 $.$

查看试题解析

三、解答题（本大题共12小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

17.
解方程：

(1)、 $2 x^{2} - 18 = 0$ ；

(2)、 $x^{2} - 4 x - 5 = 0$ ．

查看试题解析
18.
解方程：

(1)、 $5 x^{2} + 3 x = x + 1$ ；

(2)、 $x (2 x - 5) = 4 x - 10$ ．

查看试题解析
19.
二次函数图象的顶点坐标是 $(- 3 ， 2)$ ，并经过点 $(- 1 ， 0)$ ，求这个二次函数的函数关系式．

查看试题解析
20.
已知二次函数 $y = - (x + 1)^{2} + 4$ ．

(1)、在平面直角坐标系 $x O y$ 中画出该函数的图象；

(2)、当 $- 3 \leq x \leq 0$ 时，结合函数图象，直接写出 $y$ 的取值范围．

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x + 2 m - 1 = 0$ 有两个不相等的实数根．

(1)、求 $m$ 的取值范围；

(2)、若 $m$ 为正整数，且该方程的根都是整数，求 $m$ 的值．

查看试题解析
22.
已知等边三角形 $A B C$ 的边 $A B$ 、 $A C$ 的长分别是关于 $x$ 的方程 $x^{2} - m x + 9 = 0$ 的两个实数根．

(1)、求 $m$ 的值．

(2)、求 $△ A B C$ 的面积．

查看试题解析
23.
今年朝阳区在老旧小区改造方面取得了巨大成就，人居环境得到了很大改善 $.$ 某小区规划在如图宽为 $20 m$ ，长为 $32 m$ 的矩形地面上修筑同样宽的道路 $($ 图中阴影部分 $)$ ，余下的部分种上草坪 $.$ 要使草坪的面积为 $540 m^{2}$ ，求道路的宽．

查看试题解析
24.

如图，在 $△ A B C$ 中， $∠ A = 90 °$ ， $A B = 8 c m$ ， $A C = 6 c m$ ，现有动点 $P$ 从点 $B$ 出发，沿射线 $B A$ 方向运动，动点 $Q$ 从点 $C$ 出发，沿射线 $C A$ 方向运动，已知点 $P$ 的速度是 $2 c m / s$ ，点 $Q$ 的速度是 $1 c m / s$ ，它们同时出发，设运动时间是 $t s (t > 0)$ ．

(1)、当 $t = 3 s$ 时，求 $△ A P Q$ 的面积．

(2)、过多少秒时， $△ A P Q$ 的面积是 $8 c m^{2}$ ．

查看试题解析
25.

(1)、已知关于 $x$ 的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 有两个实数根．
求证：无论 $m$ 取何值，方程总有两个实数根．

(2)、若▱ $A B C D$ 的两边 $A B$ ， $A D$ 的长是已知方程的两个实数根，当 $m$ 为何值时，▱ $A B C D$ 是菱形？求此菱形的边长．

查看试题解析
26. 单板滑雪大跳台是北京冬奥会比赛项目之一，举办场地为首钢滑雪大跳台，运动员起跳后的飞行路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，从起跳到着陆的过程中，运动员的竖直高度 $y$ （单位：m）与水平距离 $x$ （单位：m）近似满足函数关系 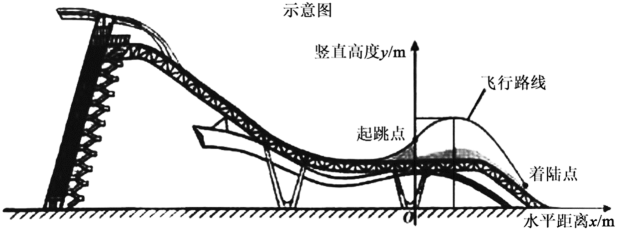$y = a (x - h)^{2} + k (a < 0)$ ．
某运动员进行了两次训练．

(1)、第一次训练时，该运动员的水平距离 $x$ 与竖直高度 $y$ 的几组数据如下：
水平距离x/m
0
2
5
8
11
14
竖直高度y/m
20.00
21.40
22.75
23.20
22.75
21.40
根据上述数据，直接写出该运动员竖直高度的最大值，并求出满足的函数关系 $y = a (x - h)^{2} + k (a < 0) ；$

(2)、第二次训练时，该运动员的竖直高度y与水平距离x近似满足函数关系 $y = - 0.04 (x - 9)^{2} + 23.24 .$ 记该运动员第一次训练的着陆点的水平距离为d₁ ，第二次训练的着陆点的水平距离为 $d_{2}$ ，则 $d_{1}$ $d_{2}$ （填“>”“=”或“<”）．

查看试题解析
27.
在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 为 $△ A B C$ 内一点，连接 $B D$ ， $D C$ ，延长 $D C$ 到点 $E$ ，使得 $C E = D C$ ．

(1)、如图 $1$ ，延长 $B C$ 到点 $F$ ，使得 $C F = B C$ ，连接 $A F$ ， $E F .$ 若 $A F ⊥ E F$ ，求证： $B D ⊥ A F$ ；

(2)、连接 $A E$ ，交 $B D$ 的延长线于点 $H$ ，连接 $C H$ ，依题意补全图 $2 .$ 若 $A B^{2} = A E^{2} + B D^{2}$ ，用等式表示线段 $C D$ 与 $C H$ 的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于已知的点 $P$ ， $Q$ ，过点 $P$ 分别作 $x$ 轴和 $y$ 轴的垂线 $l_{1}$ ， $l_{2}$ ，记点 $Q$ 到直线 $l_{1}$ 的距离为 $d_{1}$ ，点 $Q$ 到直线 $l_{2}$ 的距离为 $d_{2}$ ，若 $d_{1} \geq d_{2}$ ，则点 $Q$ 到点 $P$ 的“特征距离”为 $d_{1}$ ，若 $d_{1} < d_{2}$ ，则点 $Q$ 到点 $P$ 的“特征距离”为 $d_{2}$ ．

(1)、已知点 $A (1 ， 2)$
$①$ 点 $B (- 2 ， 3)$ 到点 $A$ 的“特征距离”为；
$②$ 点 $C$ 在函数 $y = x^{2}$ 的图象上，若点 $C$ 到点 $A$ 的“特征距离”为 $1$ ，则点 $C$ 的坐标为；

(2)、已知点 $P (3 ， 4)$ ，点 $E (a ， 0)$ ， $F (0 ， b)$ 为平面内的动点，其中 $a$ ， $b$ 均为非负数，且满足 $E F = 2 .$ 以 $E F$ 为边作正方形 $E F G H (E$ . 、 $F$ 、 $G$ 、 $H$ 按顺时针方向排列 $)$ ，记线段 $G H$ 上一动点 $Q$ 到点 $P$ 的“特征距离”为 $t$ ，直接写出 $t$ 的最大值和最小值，以及相应的 $H$ 点的坐标．

查看试题解析

水平距离x/m	0	2	5	8	11	14
竖直高度y/m	20.00	21.40	22.75	23.20	22.75	21.40