重庆市潼南区六校2023-2024学年九年级上学期第一次联考数学试题
试卷更新日期:2023-11-06 类型:月考试卷
一、单选题:(本大题10个小题,每小题4分,共40分)
-
1. 4的相反数是( )A、4 B、 C、 D、2. 下列方程是一元二次方程的是( )A、 B、 C、 D、3. 已知是一元二次方程的一个根,则的值是( )A、 B、2023 C、2022 D、20244. 已知二次函数自变量x的部分取值和对应的函数值y如下表:
x
…
0
1
2
…
y
…
5
0
…
下列说法中正确的是( )
A、函数图象开口向下 B、函数图象与x轴的交点坐标是 C、当时,y随x的增大而增大 D、顶点坐标是5. 估计的值应在( )之间A、9和10 B、8和9 C、7和8 D、6和76. 在同一平面直角坐标系中,函数与的图像可能是( )A、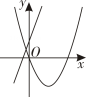 B、
B、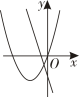 C、
C、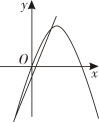 D、
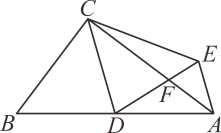
D、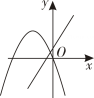 7. 已知二次函数 , 下列说法正确的是( )A、其图像的开口向下 B、其图像的对称轴为直线 C、其图像顶点坐标为 D、当时,随的增大而减小8. 我市某家快递公司,今年4月份完成投递的快递件数为2万件,4至6月份完成投递的快递件数总和为7.28万件,若该快递公司由4月份到6月份投递总件数的月平均增长率为x,则以下所列方程正确的是( )A、 B、 C、 D、9. 如图,在中, , 垂足为点的平分线交线段于点 , 若 , 则的周长为( )
7. 已知二次函数 , 下列说法正确的是( )A、其图像的开口向下 B、其图像的对称轴为直线 C、其图像顶点坐标为 D、当时,随的增大而减小8. 我市某家快递公司,今年4月份完成投递的快递件数为2万件,4至6月份完成投递的快递件数总和为7.28万件,若该快递公司由4月份到6月份投递总件数的月平均增长率为x,则以下所列方程正确的是( )A、 B、 C、 D、9. 如图,在中, , 垂足为点的平分线交线段于点 , 若 , 则的周长为( ) A、 B、 C、 D、10. 有n个依次排列的整式,第一个整式为 , 第二个整式为 , 第二个整式减去第一个整式的差记为 , 将记为 , 将第二个整式加上 , 作为第三个整式,将记为 , 将第三个整式与相加记为第四个整式,以此类推,以下结论正确的个数是( )
A、 B、 C、 D、10. 有n个依次排列的整式,第一个整式为 , 第二个整式为 , 第二个整式减去第一个整式的差记为 , 将记为 , 将第二个整式加上 , 作为第三个整式,将记为 , 将第三个整式与相加记为第四个整式,以此类推,以下结论正确的个数是( )①②当时,第四个整式的值为81③若第三个整式与第四个整式的和为25,则④第2023个整式为
A、4 B、3 C、2 D、1二、填空题:(本大题8个小题,每小题4分,共32分)
-
11. 计算12. 关于x的一元二次方程的根是 , 则的值为13. 一个多边形的内角和是外角和的4倍,则这个多边形的边数为14. 已知二次函数图像的对称轴为 , 且经过点两点,则 . (填“>”“<”或“=”)15. 某校“自然之美”研究小组在野外考察时发现一种植物的生长规律,即植物的1个主干上长出x个枝干,每个枝干又长出x个小分支,现在一株植物上有主干、枝干、小分支数量之和为73,根据题意,请列出方程为16. 关于的二次函数与轴有交点,且关于的分式方程的解为整数,则所有满足条件的整数的值之和是17. 已知中,点为斜边的中点,连接 , 将沿翻折,使点落在点的位置,交于 , 连接 . 若 , 则的长为
 18. 如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“勤劳数”.例如:630,123.最大的“勤劳数”是若三位数是“勤劳数”,且各位数字之和大于7小于10,且百位数字使得关于的一元二次方程有实数根,则满足条件的所有“勤劳数”的和是
18. 如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“勤劳数”.例如:630,123.最大的“勤劳数”是若三位数是“勤劳数”,且各位数字之和大于7小于10,且百位数字使得关于的一元二次方程有实数根,则满足条件的所有“勤劳数”的和是三、解答题:(本大题共8个小题,19小题8分,20-26每小题10分)
-
19. 按要求解方程(1)、(用适当方法)(2)、(用配方法)20. 为了更好的普及垃圾分类知识,倡导低碳生活的理念,更好地推进垃圾分类工作,梓潼中学举办了垃圾分类知识普及讲座,为了了解初一、初二两个年级对垃圾分类知识的掌握情况分别从初一、初二两个年级中随机各抽取了20名同学进行垃圾分类知识测试(测试成绩为合格),进行了整理、描述和分析,下面给出了部分信息:
初一测试成绩的扇形统计图如下(成绩分为A、B、C、D、E、F六组),其中初一测试成绩在这一组的是:;
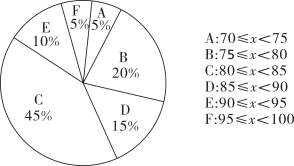
初一、初二测试成绩的平均数、中位数、众数如下:
年级
平均数
中位数
众数
初一
83
88
初二
83
87
89
根据以上信息,回答下列问题:
(1)、表中的值为(2)、如果该校初一的740名同学都参加测试,那么估计有多少名初一学生测试成绩合格?(3)、此次测试中,对垃圾分类知识的掌握情况更好地是哪个年级?请说明理由21. 是平行四边形的对角线,平分 , 交于点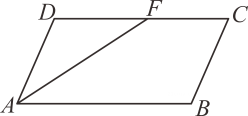 (1)、请用尺规作的平分线 , 交于点(只保留作图痕迹,不写结论,不写作法)(2)、根据图形,证明四边形为平行四边形,请完成下面的填空
(1)、请用尺规作的平分线 , 交于点(只保留作图痕迹,不写结论,不写作法)(2)、根据图形,证明四边形为平行四边形,请完成下面的填空证明:四边形是平行四边形
▲ (两直线平行,内错角相等)
平分平分
▲ , ▲
▲ ▲
又四边形是平行四边形
四边形是平行四边形 ▲ (填推理的依据)
22. 如图1,是等边三角形, , 点从点出发,以每秒1个单位长度的速度沿着运动到点停止,作交直线于点 , 设 , 点的运动时间为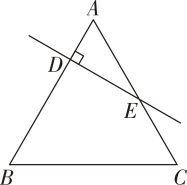 图1 (1)、直接写出与之间的函数表达式,并写出对应的取值范围(2)、在图2的平面直角坐标系中画出的图像,并写出的一条性质
图1 (1)、直接写出与之间的函数表达式,并写出对应的取值范围(2)、在图2的平面直角坐标系中画出的图像,并写出的一条性质
图2(3)、结合图像直接写出时的值.(保留一位小数,误差不超过0.2)23. 中秋节到来之际,一超市准备推出甲种月饼和乙种月饼两种月饼,计划用1200元购买甲种月饼,600元购买乙种月饼,一个甲种月饼和一个乙种月饼的进价之和为9元,且购进甲种月饼的数量是乙种月饼数量的4倍.(1)、求计划分别购买多少个甲种月饼和乙种月饼.(2)、为回馈客户,厂家推出了一系列活动,每个甲种月饼的售价降低了 , 每个乙种月饼的售价便宜了元,现在在(1)的基础上购买乙种月饼的数量增加了个,但甲种月饼和乙种月饼的总数量不变,最终的总费用比原计划减少了元,求的值.24. 北斗卫星导航系统是中国自行研制的卫星导航系统,其由空间段,地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务.如图,小敏一家自驾到风景区游玩,到达地后,导航显示车辆应沿北偏西方向行驶4千米至地,再沿北偏东方向行驶一段距离到达风景区 , 小敏发现风景区在地的北偏东方向.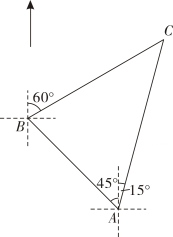 (1)、求的度数(2)、求两地的距离(如果运算结果有根号,请保留根号)25. 若直线与轴交于点 , 与轴交于点 , 二次函数的图像经过点 , 点 , 且与轴交于点
(1)、求的度数(2)、求两地的距离(如果运算结果有根号,请保留根号)25. 若直线与轴交于点 , 与轴交于点 , 二次函数的图像经过点 , 点 , 且与轴交于点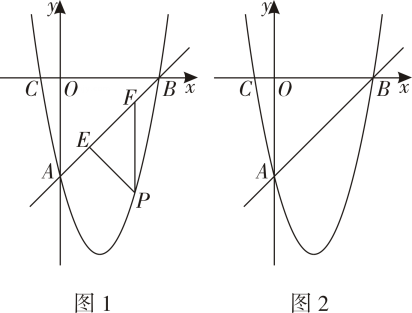 (1)、求二次函数的解析式(2)、若点为直线下方抛物线上一点,过点作直线的垂线,垂足为 , 作轴交直线于点 , 求周长的最大值及此时点的坐标(3)、将抛物线沿轴的正方向平移2个单位长度得到新抛物线是新抛物线与轴的交点(靠近轴),是原抛物线对称轴上一动点,在新抛物线上存在一点 , 使得以、、为顶点的四边形是平行四边形,请直接写出符合条件的点的坐标,并写出求解点坐标的其中一种情况的过程.26. 在中,分别为边上的两动点,
(1)、求二次函数的解析式(2)、若点为直线下方抛物线上一点,过点作直线的垂线,垂足为 , 作轴交直线于点 , 求周长的最大值及此时点的坐标(3)、将抛物线沿轴的正方向平移2个单位长度得到新抛物线是新抛物线与轴的交点(靠近轴),是原抛物线对称轴上一动点,在新抛物线上存在一点 , 使得以、、为顶点的四边形是平行四边形,请直接写出符合条件的点的坐标,并写出求解点坐标的其中一种情况的过程.26. 在中,分别为边上的两动点,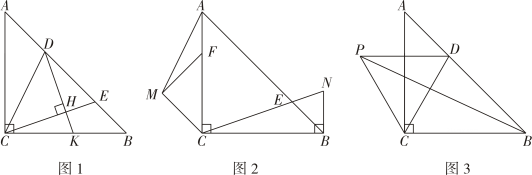 (1)、如图1,过点作分别交于点 , 当时,求证:(2)、如图2,过点作交的延长线于点 , 是边上的一动点,且 ,
(1)、如图1,过点作分别交于点 , 当时,求证:(2)、如图2,过点作交的延长线于点 , 是边上的一动点,且 ,以为斜边向左作等腰 , 连接 , 求证:
(3)、如图3,以为边向左作等边 , 连接 , 当时,且点在直线上运动时,直接写出的最小值.