山西省运城市2022-2023学年八年级上学期第一次月考数学试题

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求）

1. 2的平方根是（）

A、4 B、 $\pm 4$ C、 $\sqrt{2}$ D、 $\pm \sqrt{2}$

查看试题解析
2. 下列各组数中，是勾股数的是（）

A、8，15，17 B、 $\frac{3}{2}$ ， 2， $\frac{5}{2}$ C、1， $\sqrt{2}$ ， $\sqrt{3}$ D、4，5，6

查看试题解析
3. 在 $\sqrt{5}$ ， 3.14，2.101001000100001…（每两个1之间的0依次增加）， $π$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 已知直角三角形两边的长分别是3和4，求第三边的长.琪棋的解答过程：“当第三边是斜边时，第三边长为 $\sqrt{3^{2} + 4^{2}} = 5$ .当第三边是直角边时，第三边长为 $\sqrt{4^{2} - 3^{2}} = \sqrt{7}$ .故直角三角形第三边长是5或 $\sqrt{7}$ .”琪棋的上述方法体现的数学思想是（）

A、整体思想 B、转化思想 C、数形结合思想 D、分类讨论思想

查看试题解析
5. 下列各式中，正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt[3]{- 27} = - 3$ C、 $\sqrt{16} = 8$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
6. 估计 $\sqrt{23}$ 的值在（）

A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间

查看试题解析
7. 如图，在△ABC中， $∠ B A C = 90 °$ ， $B C = 6$ ，以AB，AC为边作正方形，这两个正方形的面积和为（）

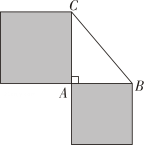A、6 B、36 C、16 D、49

查看试题解析
8. 若a是 ${(- 5)}^{2}$ 的平方根，b的一个平方根是3，则代数式 $a - b$ 的值为（）

A、－14或－4 B、－14 C、－4 D、4或－14

查看试题解析
9. 如图，圆柱形杯子底面直径为7cm，高为24cm.将一根长36cm的木棒斜放在杯中，设木棒露在杯子外面的长度为h cm，则h的最小值是（）

A、9 B、11 C、12 D、14

查看试题解析
10. 如图，ABCD是长方形地面，长AB＝10m，宽AD＝5m，中间刚好有一堵墙，墙高MN＝1m，一只蜗牛从A点爬到C点，它必须翻过中间那堵墙，则它至少要走（）

A、10m B、12m C、13m D、14m

查看试题解析

二、填空题（本大题共5个小题，每小题3分，共15分）

11. 比较大小： $- \sqrt{3}$ －2.（填“＞”或“＜”）

查看试题解析
12. $\sqrt{64}$ 的立方根是．

查看试题解析
13. 如图，在△ABC中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 5$ ，则AB的长为.

查看试题解析
14. 定义新运算“☆”： $a ☆ b = \sqrt{a b + 1}$ .则 $6 ☆ (3 ☆ 5) =$ .

查看试题解析
15. 如图，△ABC的顶点在边长为1的正方形网格的格点上， $C D ⊥ A B$ 于点D，则BD的长为.

查看试题解析

三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

16.

(1)、计算： $\sqrt{9} - \sqrt[3]{- 27} + | - \sqrt{3} | + {(π - 3)}^{0}$ .

(2)、求x的值： $8 {(x - 1)}^{3} - 27 = 0$ .

查看试题解析
17. 如图，5×5方格中每个小正方形的边长都为1.

(1)、图（1）中正方形ABCD的面积为，边长为.
图（1）

(2)、在图（2）的数轴上，用圆规找出实数 $\sqrt{17} - 1$ 的准确位置.
图（2）

查看试题解析
18. 如图，在海面上有两个疑似漂浮目标A、B，接到消息后，两艘搜救艇同时从港口O出发赶往目的地.一艘搜救艇以6海里/时的速度沿北偏东60°的方向向目标A前进，同时另一艘搜救艇以8海里/时的速度向目标B前进，1.5小时后，他们同时分别到达目标A、B，此时，他们相距15海里，请问第二艘搜救艇的航行方向是北偏西多少度？

查看试题解析
19. 已知实数 $2 x - 1$ 和 $x - 5$ 是正数a的两个平方根.

(1)、求x和a的值.

(2)、求 $6 x - 4$ 的立方根.

查看试题解析

20. 阅读与思考

阅读下面的文字，并完成相应的任务.

大家知道 $\sqrt{7}$ 是无理数，而无理无限不循环小数，因此 $\sqrt{7}$ 的小数部分我们不可能全部写出来，我们可以减去它的整数部分就可以得到小数部分，于是我们需要先对这个数进行估值.因为 $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，所以 $\sqrt{7}$ 的整数部分为2，小教部分为 $\sqrt{7} - 2$ .

任务：已知a是 $\sqrt{17} - 3$ 的整数部分，b是 $\sqrt{17} - 3$ 的小数部分.

(1)、求a，b的值.

(2)、求

{(- a)}^{3} + {(b + 4)}^{2}

的算术平方根.

查看试题解析

21. 如图，在一条东西走向的河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，村庄C为方便村民取水，决定在河边新建一个取水点H（点A，H，B在同一条直线上），并新修一条路CH，测得BC＝2千米，CH＝1.6千米，BH＝1.2千米.

(1)、CH是不是从村庄C到河边的最短路线？请通过计算加以说明.

(2)、求原来路线AC的长.

查看试题解析
22. 综合与实践
问题情境：某消防队在一次应急演练中，消防员架起一架长25m的云梯AB，如图，云梯斜靠在一面墙上，这时云梯底端距墙脚的距离BC＝7m，∠DCE＝90°.

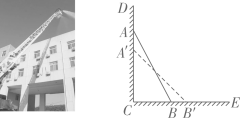(1)、独立思考：这架云梯顶端距地面的距离AC有多高？

(2)、深入探究：消防员接到命令，按要求将云梯从顶端A下滑到A＇位置上（云梯长度不改变），AA＇＝4m，那么它的底部B在水平方向滑动到B＇的距离BB＇也是4m吗？若是，请说明理由；若不是，请求出BB＇的长度.

(3)、问题解决：演练中，高24.3m的墙头有求救声，消防员需调整云梯去救援被困人员.经验表明，云梯靠墙摆放时，如果云梯底端离墙的距离不小于云梯长度的 $\frac{1}{5}$ ，则云梯和消防员相对安全.在相对安全的前提下，云梯的顶端能否到达24.3m高的墙头去救援被困人员？

查看试题解析
23. 综合与实践
如图，在△ABC中，AB＝10，BC＝6，AC＝8.

(1)、猜想：请判断△ABC的形状并说明理由.

(2)、探究：如果点P从点A出发，以每秒4个单位长度的速度沿折线A-C-B-A方向运动，运动到点A停止，设运动时间为t（ $t > 0$ ）秒.

①若点P在AC上，且满足PA＝PB，求此时t的值.
②若点P恰好在△BAC的平分线上，求t的值.

查看试题解析