四川省成都市东部新区联考2023-2024学年八年级上学期10月课堂监测数学试题

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8个小题，每小题4分，共32分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列各数： $0.4 \overset{•}{5} \overset{•}{6}$ ， $\frac{3 π}{2}$ ， 3.14，0.80108， $π - | 1 - π |$ ， 0.1010010001…， $\sqrt{4}$ ， 0.451452453454…，其中无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. $\sqrt{5} - 1$ 介于（）

A、－1和0之间 B、0和1之间 C、1和2之间 D、2和3之间

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（　　）

A、4，5，6 B、3，4，5 C、2，3，4 D、1，2，3

查看试题解析
4. 下列二次根式中，能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{48}$ C、 $\sqrt{20}$ D、 $\sqrt{18}$

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $| - 3 | = - 3$ C、 $- \sqrt{9} = - 3$ D、 $- 3^{2} = 9$

查看试题解析
6. 在函数 $y = \frac{\sqrt{x + 2}}{x}$ 中，自变量x的取值范围是（）

A、 $x \geq - 2$ 且 $x \neq 0$ B、 $x > - 2$ 且 $x \neq 0$ C、 $x > 0$ D、 $x \leq - 2$

查看试题解析
7. 如果 $a b > 0$ ， $a + b < 0$ ，那么下面各式：① $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ ， ② $\sqrt{\frac{a}{b}} \times \sqrt{\frac{b}{a}} = 1$ ， ③ $\sqrt{a b} \div \sqrt{\frac{a}{b}} = - b$ ，其中正确的是（）.

A、①② B、②③ C、①③ D、①②③

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = A C = 10$ ， $B C = 16$ ，点P是BC边上的动点，过点P作 $P D ⊥ A B$ 于点D， $P E ⊥ A C$ 于点E，则 $P D + P E$ 的长是（）

A、7.6 B、10 C、9.6或7.6 D、9.6

查看试题解析

二、填空题（每小题4分，共20分）

9. $\sqrt{16}$ 的平方根是．

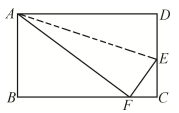
查看试题解析
10. 一根高16米的旗杆在台风中断裂，旗杆顶部落在离旗杆底部8米处，旗杆折断处离地面高为．

查看试题解析
11. 已知 $a \geq - 1$ ，化简 $\sqrt{a^{2} + 2 a + 1}$ =;

查看试题解析
12. 比较下列实数的大小（填“＞”“＜”或“＝”）．

(1)、 $\sqrt{40}$ 12；

(2)、 $\frac{\sqrt{5} - 1}{2}$ 0.5．

查看试题解析
13. 如图，将长方形ABCD的长AD沿折痕AE折叠，使点D落在BC上的F处，若 $A B = 6$ ， $A D = 10$ ，则 $B F =$ ．

查看试题解析

三、解答题（共48分）

14. 计算：

(1)、 $\sqrt{27} - 2 \sqrt{3} + \sqrt{48}$ ．

(2)、 $\sqrt[3]{- 8} + (π - 3)^{0} - | 1 - \sqrt{2} | + \frac{1}{\sqrt{2} + 1}$ ．

查看试题解析
15. 已知 $a = \frac{1}{\sqrt{5} + 2}$ ， $b = \frac{1}{\sqrt{5} - 2}$ ．

(1)、化简a，b；

(2)、求 $a^{2} - 4 a b + b^{2}$ 的值．

查看试题解析
16. 如图所示，已知等腰三角形ABC的底边BC=20cm，D是腰AB上一点，且CD=16cm，BD=12cm，求△ABC的周长．

查看试题解析
17. 某中学A，B两栋教学楼之间有一块如图8所示的四边形空地ABCD，学校为了绿化环境，计划在空地上种植花草，经测量 $∠ A B C = 90 °$ ， $A B = 20$ 米， $B C = 15$ 米， $C D = 7$ 米， $A D = 24$ 米．

(1)、求出四边形空地ABCD的面积；

(2)、若每种植1平方米的花草需要投入120元，求学校共需投入多少元．

查看试题解析
18. 如图，四边形ABCD中， $A D / / B C$ ， $∠ B A D = 90 °$ ，点M为AB上一点，连接CM，DM．

(1)、求证： $∠ C M D = ∠ B C M + ∠ A D M$ ；

(2)、若 $A D = 8$ ， $A M = 6$ ， $C D = C M = 5 \sqrt{2}$ ，求四边形AMCD的面积；

(3)、在（2）的情况下，连接AC，求AC的长．

查看试题解析

四、填空题（共5小题，每小题4分，满分20分）

19. 已知： $y = \frac{\sqrt{x - 5} + \sqrt{5 - x}}{3} - 2$ ，则 $x^{y} =$ ．

查看试题解析
20. 计算： ${(\sqrt{3} - 2)}^{2019} \times {(\sqrt{3} + 2)}^{2020} =$ ．

查看试题解析
21. $△ A B C$ 中， $A B = 10$ ， $A C = 17$ ， BC边上的高 $A D = 8$ ，则线段BC的长为．

查看试题解析
22. 边长分别为4cm，3cm两正方体如图放置，点P在 $E_{1} F_{1}$ 上，且 $E_{1} P = \frac{1}{3} E_{1} F_{1}$ ，一只蚂蚁如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是cm．

查看试题解析
23. 如图，锐角三角形ABC中， $∠ C = 2 ∠ B$ ， $A B = 2 \sqrt{6}$ ， $B C + C A = 8$ ，则 $△ A B C$ 的面积为．

查看试题解析

五、解答题（共3小题，满分30分）

24. 已知a、b为有理数，m、n分别表示 $6 - \sqrt{13}$ 的整数部分和小数部分，且 $a m + b n = 6 + \sqrt{13}$ ，求 $2 a - 8 b$ 的平方根．

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，把 $△ A B C$ 沿直线DE折叠，使点A与点B重合，若 $△ B C E$ 的周长为 $m (m > 0)$ ， $A B = n (n > 0)$ ，求 $△ A B C$ 的面积．（用含m，n的代数式表示）

查看试题解析
26. 若实数x，y满足 $(x - \sqrt{x^{2} - 2016}) (y - \sqrt{y^{2} - 2016}) = 2016$ ．

(1)、求x，y之间的数量关系；

(2)、求 $3 x^{2} - 2 y^{2} + 5 x - 5 y - 2019$ 的值．

查看试题解析