四川省成都东部新区联考2023-2024学年九年级上学期10月课堂监测数学试题

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1. 下列方程是一元二次方程的是（）

A、 $x + 2 y = 1$ B、 $x^{2} = 1$ C、 $x^{2} + \frac{3}{x} = 8$ D、 $x (x + 3) = x^{2} - 1$

查看试题解析
2. 将方程 $x^{2} - 6 x + 3 = 0$ 左边配成完全平方式，得到的方程是（）

A、 ${(x - 3)}^{2} = - 3$ B、 ${(x - 3)}^{2} = 6$ C、 ${(x - 3)}^{2} = 3$ D、 ${(x - 3)}^{2} = 12$

查看试题解析
3. 下列说法正确的是（）

A、对角线互相垂直的四边形是菱形 B、矩形对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、对角线相等的菱形是正方形

查看试题解析
4. 已知一元二次方程 $x^{2} + k x + 3 = 0$ 有一个根为3，则k的值为（）

A、－4 B、4 C、－2 D、2

查看试题解析
5. 如图，菱形ABCD中，对角线AC，BD相交于点O，点M是DC的中点.若菱形ABCD的周长为24，则 $O M$ 的长为（）

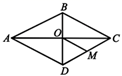A、12 B、8 C、6 D、3

查看试题解析
6. 若关于x的方程 $k x^{2} + 2 x + 1 = 0$ 有实数根，则实数k的取值范围是（）

A、 $k \neq 0$ B、 $k \leq 1$ C、 $k < 1$ D、 $k \leq 1$ 且 $k \neq 0$

查看试题解析
7. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O， $D E ⊥ A B$ 于点E，若 $A C = 8 c m$ ， $B D = 6 c m$ ，则 $D E =$ （）

A、 $5 \sqrt{3} c m$ B、 $2 \sqrt{5} c m$ C、 $\frac{24}{5} c m$ D、 $\frac{48}{5} c m$

查看试题解析
8. 如图，矩形ABCD中， $A B = 8 c m$ ， $A D = 6 c m$ ， EF是对角线BD的垂直平分线，则EF的长为（）

A、 $\frac{15}{4} c m$ B、5cm C、 $\frac{15}{2} c m$ D、8cm

查看试题解析

二、填空题（本大题共5个小题，每小题4分，共20分，）

9. 若将方程 $x^{2} + 8 x = 7$ 化为 ${(x + m)}^{2} = 23$ ，则 $m =$ ．

查看试题解析
10. 如图，菱形ABCD的两条对角线相交于O，若AC=8，BD=6，则菱形ABCD的周长是．

查看试题解析
11. 关于x的一元二次方程 $(m - 3) x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
12. 已知 $x_{1}$ ， $x_{2}$ 是关于x的一元二次方程 $x^{2} + 3 x + k - 1 = 0$ 的两个实数根，且 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 15$ ，则k的值为．

查看试题解析
13. 如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上一个动点，则PF+PE的最小值为．

查看试题解析

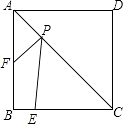
三、解答题（本大题共5个小题，共48分，解答过程写在答题卡上）

14.

(1)、计算： $\sqrt{12} + {(- \frac{1}{2})}^{- 1} + | 2 \sqrt{3} - 5 | - (\sqrt{3} + 2)^{0}$ ；

(2)、解方程： $3 {(x - 3)}^{2} = x^{2} - 9$ ．

查看试题解析
15. 已知一元二次方程 $x^{2} - 4 x + k = 0$ 有两个不相等的实数根．

(1)、求k的取值范围；

(2)、如果k是符合条件的最大整数，且一元二次方程 $x^{2} - 4 x + k = 0$ 与 $x^{2} + m x - 1 = 0$ 有一个相同的根，求此时m的值．

查看试题解析
16. 如图，在矩形ABCD中，E为AB边上一点，EC平分 $∠ D E B$ ， F为CE的中点，连接AF，BF，过点E作 $E H / / B C$ 分别交AF，CD于G，H两点．

(1)、求证： $D E = D C$ ；

(2)、求证： $A F ⊥ B F$ ；

查看试题解析
17. 已知：关于x的一元二次方程 $k x^{2} - (3 k - 1) x + 2 (k - 1) = 0$ ．若此方程有两个实数根 $x_{1}$ 、 $x_{2}$ ，且 $| x_{1} - x_{2} | = 2$ ，求k的值．

查看试题解析
18. 如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将 $△ A B E$ 沿AE所在直线折叠，点B的对应点是点 $B^{'}$ ，连接 $A B^{'}$ 并延长交直线DC于点F．

(1)、当点F与点C重合时如图（1），证： $D F + B E = A F$ ．

(2)、当点F在DC的延长线上时如图（2），当点F在CD的延长线上时如图（3），线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．

查看试题解析

四、填空题（本大题共5个小题，每小题4分，共20分，）

19. 设m，n是一元二次方程 $x^{2} + 3 x - 5 = 0$ 的两个根，则 $m^{2} + 7 m + 4 n$ 的值为．

查看试题解析
20. 关于 $x$ 的方程 $a {(x + m)}^{2} + b = 0$ 的解是 $x_{1}$ = $2$ ， $x_{2}$ = $- 1$ （ $a$ 、 $b$ 、 $m$ 为常数， $a \neq$ 0），则方程 $a {(x + m + 2)}^{2} + b = 0$ 的解是．

查看试题解析
21. 如图，四边形ABCD是菱形，BD＝4 $\sqrt{2}$ ， AD＝2 $\sqrt{6}$ ，点E是CD边上的一动点，过点E作EF⊥OC于点F ， EG⊥OD于点G ，连接FG ，则FG的最小值为．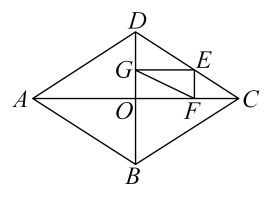

查看试题解析
22. 正方形ABCD的边长是8cm，点M在BC边上，且MC=2cm，P是正方形边上的一个动点，连接PB交AM于点N，当PB=AM时，PN的长是．

查看试题解析
23. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ 有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有．
①方程 $x^{2} - x - 2 = 0$ 是倍根方程；
②若 $(x - 2) (m x + n) = 0$ 是倍根方程，则 $4 m^{2} + 5 m n + n^{2} = 0$ ；
③若p、q满足 $p q = 2$ ，则关于x的方程 $p x^{2} + 3 x + q = 0$ 是倍根方程；
④若方程 $a x^{2} + b x + c = 0$ 是倍根方程，则必有 $2 b^{2} = 9 a c$ ．

查看试题解析

五、解答题（本大题共3个小题，共30分，解答应写出必要的文字说明．证明过程或演算步骤）

24. 某水果店经销一种高档水果，进价为每千克40元，售价为每千克60元，每天可售出300千克．经市场调查发现，若该水果售价每千克降价1元，日销售量将增加20千克．设该水果每千克降价x元．

(1)、降价后，每千克水果盈利元，每天可销售千克；（用含x的代数式表示）

(2)、现商家为了保证销售该水果每天盈利6120元，且尽量让顾客获得优惠，那么每千克应降价多少元？

查看试题解析
25. 如图，四边形ABCD是正方形， $△ E F C$ 是等腰直角三角形，点E在AB上，且 $∠ C E F = 90 °$ ， $F G ⊥ A D$ ，垂足为点G．

(1)、试判断AG与FG是否相等？并给出证明；

(2)、若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．

查看试题解析
26. 如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（ $O A < O B$ ）且OA、OB的长分别是一元二次方程 $x^{2} - (\sqrt{3} + 1) x + \sqrt{3} = 0$ 的两个根，点C在x轴负半轴上，且 $A B ： A C = 1 ： 2$ ．

(1)、求A、C两点的坐标；

(2)、若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设 $△ A B M$ 的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；

(3)、点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．

查看试题解析