山西省晋中市平遥县2023-2024学年九年级上学期数学月考考试试卷

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、单项选择题（共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求）

1. 下列方程是一元二次方程的是（）

A、x（x＋3）＝0 B、x²－4y＝0 C、 $x^{2} - \frac{3}{x} = 5$ D、ax²＋bx＋c＝0（a ， b ， c为常数）

查看试题解析
2. 下列四个菱形中分别标注了部分数据，根据所标数据，可以判断菱形是正方形的是（）

A、 B、 C、 D、

查看试题解析
3. 某中学组织九年级学生篮球比赛，以班为单位，每两班之间都比赛一场，总共安排15场比赛，则共有多少个班级参赛（）

A、6 B、5 C、4 D、3

查看试题解析
4. 下列用配方法解方程 $\frac{1}{2} x^{2} - x - 2 = 0$ 的四个步骤中，出现错误的是（）

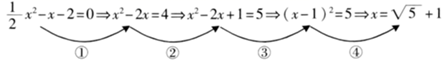A、① B、② C、③ D、④

查看试题解析
5. 如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为CD的中点.若OE＝3，则菱形ABCD的周长为（）

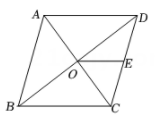A、6 B、12 C、24 D、48

查看试题解析
6. 如图，在菱形ABCD中，对角线AC ， BD相交于点O ，若∠BAD＝110°，则∠OBC的度数为（）

A、30° B、35° C、55° D、70°

查看试题解析
7. 一元二次方程 $x^{2} - 3 \sqrt{2} x + 3 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、有一个实数根 D、无实数根

查看试题解析
8. 如图矩形与正方形的形状有差异，我们将矩形与正方形的接近程度称为矩形的“接近度”，已知矩形ABCD的对角线AC ， BD相交于点O ，我们将矩形的“接近度”定义为 $\frac{A B^{2}}{B C^{2}}$ ，若∠BOC＝60°时，则矩形的“接近度”为（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{1}{\sqrt{3}}$ D、 $\sqrt{3}$

查看试题解析
9. 如图，某小区计划在一个长16m，宽9m的矩形场地ABCD上，修建三条同样宽的小路，竖直的与AB平行，水平的与AD平行，其余部分种草，已知草坪部分的总面积为112m² ，设小路宽xm，则x满足的方程为（）

A、x²－17x－16＝0 B、x²－17x＋16＝0 C、x²＋17x－16＝0 D、x²＋17x＋16＝0

查看试题解析
10. 如图，在矩形ABCD中，AB＝8，BC＝4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）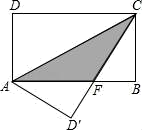

A、6 B、8 C、10 D、12

查看试题解析

二、填空题（共5个小题，每小题3分，共15分）

11. 方程x²－5x＝0的解是.

查看试题解析
12. 若把代数式x²-4x-5化成(x-m)²+k的形式，其中m，k为常数，则m+k=

查看试题解析
13. 如图矩形ABCD在平面直角坐标系中，若顶点A、B、D在坐标轴上，AB＝6，∠ABD＝60°，则点D的坐标．

查看试题解析
14. 某药品原价每盒100元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒64元，则该药品平均每次降价的百分率是．

查看试题解析
15. 如图，已知正方形ABCD边长是6，点P是线段BC上一动点，过点D作DE⊥AP于点E ．连接EC ，若CE＝CD ，则线段DE的长度是．

查看试题解析

三、解答题（共8个小题，共75分，解答应写出必要的文字说明、证明过程或演算步骤）

16. 选择适当的方法解方程：

(1)、x²＋8x＋4＝0

(2)、（2x＋1）²－4x－2＝0

查看试题解析

17. 小敏与小霞两位同学解方程3（x－3）＝（x－3）²的过程如下框：

小敏：两边同除以（x－3），得3＝x－3，

则x＝6．

小霞：移项，得3（x－3）－（x－3）²＝0，

提取公因式，得（x－3）（3－x－3）＝0．

则x－3＝0或3－x－3＝0，

解得x₁＝3，x₂＝0．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

18. 如图，矩形ABCD的对角线AC，BD相交于点O，且DE∥AC，CE∥BD．试判断四边形OCED的形状并证明．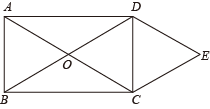

查看试题解析
19. 平安路上，多“盔”有你，在“交通安全宣传月”期间，某商店销售一批头盔，进价为每顶 $40$ 元，售价为每顶 $68$ 元，平均每周可售出 $100$ 顶 $．$ 商店计划将头盔降价销售，每顶售价不高于 $58$ 元，经调查发现：每降价 $2$ 元，平均每周可多售出 $40$ 顶 $．$ 设每顶头盔降价 $x$ 元，平均每周的销售量为 $y$ 顶．

(1)、平均每周的销售量 $y ($ 顶 $)$ 与降价 $x ($ 元 $)$ 之间的函数关系式是；

(2)、若售价为每顶 $50$ 元，求每周的销售利润；

(3)、若该商店希望平均每周获得 $4000$ 元的销售利润，则每顶头盔应降价多少？

查看试题解析
20. 如图，在△ABC中，D是BC边上一点，E是AD的中点，过A作BC的平行线交CE的延长线F ，且AF＝BD ，连接BF ．

(1)、求证：BD＝CD；

(2)、如果AB＝AC ，试判断四边形AFBD的形状，并证明你的结论；

(3)、当△ABC满足时，四边形AFBD为正方形（直接写出）．

查看试题解析
21. 阅读材料，解答问题：
解方程：（4x－1）²－10（4x－1）＋24＝0．
解：把4x－1视为一个整体，设4x－1＝y ，
则原方程可化为y²－10y＋24＝0．
解得y₁＝6，y₂＝4．
∴4x－1＝6或4x－1＝4．
∴ $x_{1} = \frac{7}{4} ， x_{2} = \frac{5}{4}$ ，
以上方法就叫换元法，达到简化或降次的目的，体现了转化的思想．
请仿照材料解下列方程：

(1)、（3x－5）²＋4（3x－5）＋3＝0．

(2)、x⁴－x²－6＝0．

查看试题解析
22. 在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E ， F ， G ， H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题时，有如下思路：连接AC ．
结合小敏的思路作答：

(1)、若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决问题；
图1 图2

(2)、如图2，在（1）的条件下，若连接AC ， BD ．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

查看试题解析
23.
已知四边形ABCD和AEFG均为正方形．
图1 图2

(1)、观察猜想：如图1所示，当点A、B、G三点在一条直线上时，连接BE、DG ，则线段BE与DG的数量关系是，位置关系是．

(2)、类比探究：如图2所示，将正方形AEFG在平面内绕点A逆时针旋转到图2时，则（1）的结论是否成立，若成立，请证明，若不成立，请说明理由；

(3)、拓展延伸：在（2）的条件下，将正方形AEFG在平面内绕点A任意旋转，若AE＝2，AB＝5，则BE的最大值和最小值分别是多少．

查看试题解析