山东省聊城市冠县重点学校2023-2024学年八年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-11-06 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中,对称轴最多的图形是( )A、
 B、
B、 C、
C、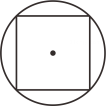 D、
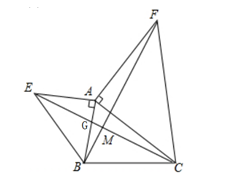
D、 2. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,若 , 为了使白球反弹后能将黑球直接撞入底袋中,那么击打白球时,必须保证为( )
2. 数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,若 , 为了使白球反弹后能将黑球直接撞入底袋中,那么击打白球时,必须保证为( ) A、 B、 C、 D、3. 到三角形的三个顶点距离相等的点是( )A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点4. 如图,在和中,已知 , 还需添加两个条件才能使≌ , 添加的一组条件不正确的是( )
A、 B、 C、 D、3. 到三角形的三个顶点距离相等的点是( )A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点4. 如图,在和中,已知 , 还需添加两个条件才能使≌ , 添加的一组条件不正确的是( ) A、 , B、 , C、 , D、 ,5. 已知线段 , , , 求作 , 使 , , , 下面作法的合理顺序为( )
A、 , B、 , C、 , D、 ,5. 已知线段 , , , 求作 , 使 , , , 下面作法的合理顺序为( )
分别以 , 为圆心, , 为半径作弧,两弧交于点;
作直线 , 在上截取;
连接 , , 为所求作的三角形.A、 B、 C、 D、6. 如图所示,将一张长方形纸片沿折叠,使顶点、分别落在点、处,交于点 , , 则( ) A、 B、 C、 D、7. 如图, , , 平分 , , 交延长线于 , 且垂足 , 则以下结论:;;;正确的个数是( )
A、 B、 C、 D、7. 如图, , , 平分 , , 交延长线于 , 且垂足 , 则以下结论:;;;正确的个数是( ) A、个 B、个 C、个 D、个8. 如图,在中, , 分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点和点 , 作直线分别交、于点和点 , 若 , 则的度数是( )
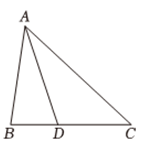
A、个 B、个 C、个 D、个8. 如图,在中, , 分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点和点 , 作直线分别交、于点和点 , 若 , 则的度数是( )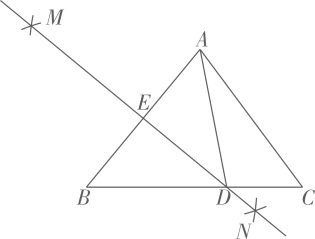 A、 B、 C、 D、9. 如图,在中, , 于点E , , , 则的度数为( )
A、 B、 C、 D、9. 如图,在中, , 于点E , , , 则的度数为( )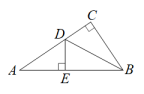 A、34° B、36° C、38° D、40°10. 如图,在中, , 的平分线交于点 , 过点作交于点 , 交于点若 , , , 则的周长是( )
A、34° B、36° C、38° D、40°10. 如图,在中, , 的平分线交于点 , 过点作交于点 , 交于点若 , , , 则的周长是( ) A、 B、 C、 D、11. 如图,在中, , , , 是的平分线,设和的面积分别是 , , 则:的值为( )
A、 B、 C、 D、11. 如图,在中, , , , 是的平分线,设和的面积分别是 , , 则:的值为( ) A、: B、: C、: D、:12. 如图,在中, , , 以点为圆心,任意长为半径画弧分别交 , 于点和 , 再分别以 , 为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长,交于点 , 则下列结论不正确的是( )
A、: B、: C、: D、:12. 如图,在中, , , 以点为圆心,任意长为半径画弧分别交 , 于点和 , 再分别以 , 为圆心,大于的长为半径画弧,两弧交于点 , 连接并延长,交于点 , 则下列结论不正确的是( ) A、平分 B、 C、点在的垂直平分线上 D、::
A、平分 B、 C、点在的垂直平分线上 D、::二、填空题(本大题共5小题,共15.0分)
-
13. 在平面直角坐标系中,若点与点关于轴对称,则点位于第 象限.14. 如图,小明站在堤岸的A点处,正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C、D间的距离为90米,则在A点处小明与游艇的距离为米.
 15. 如图,在中,边上的两点 , 分别在 , 的垂直平分线上,若 , 则的周长为 .
15. 如图,在中,边上的两点 , 分别在 , 的垂直平分线上,若 , 则的周长为 .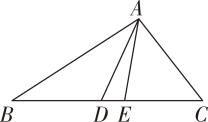 16. 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .
16. 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 .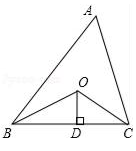 17. 如图,为坐标原点,的两个顶点 , , 点在边上,点在边上,且 , 点为边上的动点,则的最小值为 .
17. 如图,为坐标原点,的两个顶点 , , 点在边上,点在边上,且 , 点为边上的动点,则的最小值为 .
三、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
 19. 如图, , , . , 与 交于点 .
19. 如图, , , . , 与 交于点 .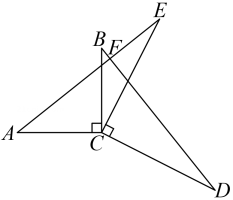 (1)、求证: ;(2)、求 的度数.20. 如图,在四边形中, , 为的中点,连接、 , , 延长交的延长线于点已知 , .
(1)、求证: ;(2)、求 的度数.20. 如图,在四边形中, , 为的中点,连接、 , , 延长交的延长线于点已知 , . (1)、求证:;
(1)、求证:;
(2)、求的长.21. 在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm. (1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
(1)、求BC的长;(2)、分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.