北京市朝阳区重点中学2023-2024学年八年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-11-06 类型:月考试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图,用三角板作 的边 上的高线,下列三角板的摆放位置正确的是( )A、
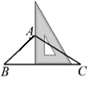 B、
B、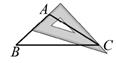 C、
C、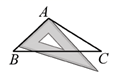 D、
D、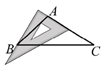 2. 十二边形的内角和为( )A、180° B、360° C、1800° D、无法计算3. 如图,和相交于点 , 则下列结论正确的是( )
2. 十二边形的内角和为( )A、180° B、360° C、1800° D、无法计算3. 如图,和相交于点 , 则下列结论正确的是( ) A、 B、 C、 D、4. 如图,已知 , 那么添加下列一个条件后,仍无法判定≌的是( )
A、 B、 C、 D、4. 如图,已知 , 那么添加下列一个条件后,仍无法判定≌的是( ) A、 B、 C、 D、5. 下列判定两直角三角形全等的方法,错误的是( )A、两条直角边对应相等 B、斜边和一直角边对应相等 C、两个锐角对应相等 D、斜边和一锐角对应相等6. 根据下列已知条件,能画出唯一的的是( )A、 , , B、 , , C、 , , D、 , ,7. 下列是真命题的是( )A、对顶角相等 B、两边和一角对应相等的两个三角形全等
A、 B、 C、 D、5. 下列判定两直角三角形全等的方法,错误的是( )A、两条直角边对应相等 B、斜边和一直角边对应相等 C、两个锐角对应相等 D、斜边和一锐角对应相等6. 根据下列已知条件,能画出唯一的的是( )A、 , , B、 , , C、 , , D、 , ,7. 下列是真命题的是( )A、对顶角相等 B、两边和一角对应相等的两个三角形全等
C、三角形的外角大于内角 D、两条直线被第三条直线所截,同位角相等8. 如图, , 点在上,且 , 点到射线的距离为 , 点在射线上, . 若的形状,大小是唯一确定的,则的取值范围是( ) A、或 B、 C、 D、或
A、或 B、 C、 D、或二、填空题(本大题共8小题,共24.0分)
-
9. 如图所示的网格是正方形网格,点 , , , 均在格点上,则 填“”,“”或“=” .
 10. 赵师傅在做完门框后,为防止变形,如图中所示的那样在门上钉上两条斜拉的木条即图中的 , 两根木条 , 这其中的数学原理 .
10. 赵师傅在做完门框后,为防止变形,如图中所示的那样在门上钉上两条斜拉的木条即图中的 , 两根木条 , 这其中的数学原理 . 11. 如图是由射线、、、组成的平面图形,则°.
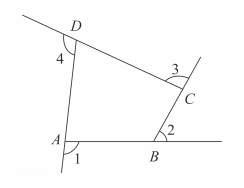
11. 如图是由射线、、、组成的平面图形,则°.
 12. 如图,在中, , , , 平分则的度数为 .
12. 如图,在中, , , , 平分则的度数为 .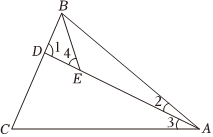 13. 如图,已知是的中线,且 , , 则和的周长之差为 ,和的面积之差为 .
13. 如图,已知是的中线,且 , , 则和的周长之差为 ,和的面积之差为 . 14. 如图,已知 , 若以“”为依据证明≌ , 还需要添加的条件是 .
14. 如图,已知 , 若以“”为依据证明≌ , 还需要添加的条件是 . 15. 甲乙两位同学进行一种数学游戏游戏规则是:两人轮流对及对应的边或角添加等量条件点 , , 分别是点 , , 的对应点某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
15. 甲乙两位同学进行一种数学游戏游戏规则是:两人轮流对及对应的边或角添加等量条件点 , , 分别是点 , , 的对应点某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.轮次
行动者
添加条件
甲
乙
甲
上表记录了两人游戏的部分过程,则下列说法正确的是 填写所有正确结论的序号 .
若第轮甲添加 , 则乙获胜;
若甲想获胜,第轮可以添加条件;
若乙想获胜,可修改第轮添加条件为 .16. 如图,平面中两条直线和相交于点 , 对于平面上任意一点 , 若点到直线、的距离分别是、 , 则称有序实数对是点的“距离坐标”特别地,当点在直线上时,定义点到直线的距离为下列说法:
“距离坐标”是的点只有点;
“距离坐标”是的点只有个;
“距离坐标”是的点共有个;
正确的有 填序号 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知:如图,点是线段上一点, , , 求证: .
 18. 如图,在中, , , 的平分线交于点 .
18. 如图,在中, , , 的平分线交于点 . (1)、尺规作图:作的平分线交于点保留作图痕迹,不写作法
(1)、尺规作图:作的平分线交于点保留作图痕迹,不写作法
(2)、求的度数.19. 如图,在中, , 是边上的两点,有下面四个关系式:① , , ③ , ④ .
请用其中两个作为已知条件,余下两个作为求证的结论,写出你的已知和求证,并证明.
已知:
求证:
证明:20. 在证明等腰三角形的判定定理时,甲、乙、丙三位同学各添加一条辅助线,方法如图所示你能用哪位同学添加辅助线的方法完成证明,请选择一种方法补全证明过程.等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等简写成“等角对等边”
已知:如图,在中,求证: .
甲的方法:
证明:作的平分线交于点 .
乙的方法:
证明:作于点 .
丙的方法:
证明:取中点 , 连接 . 21. 如图,已知 , , , , 与相交于点 .
21. 如图,已知 , , , , 与相交于点 . (1)、求证:;(2)、求证: .22. 课上,老师提出了这样一个问题:
(1)、求证:;(2)、求证: .22. 课上,老师提出了这样一个问题:
已知:如图, , 请你再添加一个条件,使得≌ . (1)、同学们认为可以添加的条件并不唯一,你添加的条件是 , 并完成证明(2)、若添加的条件是 , 证明:≌ .23. 如图,在中,点在边上,连接 , 是中边上的高线,延长交于点设 , .
(1)、同学们认为可以添加的条件并不唯一,你添加的条件是 , 并完成证明(2)、若添加的条件是 , 证明:≌ .23. 如图,在中,点在边上,连接 , 是中边上的高线,延长交于点设 , . (1)、当时,的度数为 ;(2)、求的度数用含、的式子表示;(3)、若 , 求的值.24. 【提出问题】
(1)、当时,的度数为 ;(2)、求的度数用含、的式子表示;(3)、若 , 求的值.24. 【提出问题】
我们已经知道了三角形全等的判定方法和直角三角形全等的判定方法 , 请你继续对“两边分别相等且其中一组等边的对角相等的两个三角形”的情形进行探究.
【探索研究】
已知:在和中, , , .(1)、如图 , 当时,根据 , 可知≌; (2)、如图 , 当时,请用直尺和圆规作作出 , 通过作图,可知与全等.填“一定”或“不一定”
(2)、如图 , 当时,请用直尺和圆规作作出 , 通过作图,可知与全等.填“一定”或“不一定” (3)、如图 , 当时,与是否全等?若全等,请加以证明:若不全等,请举出反例.
(3)、如图 , 当时,与是否全等?若全等,请加以证明:若不全等,请举出反例. (4)、【归纳总结】
(4)、【归纳总结】如果两个三角形的两边分别相等且其中一组等边的对角相等,那么当这组对角是
时,这两个三角形一定全等.填序号
锐角;直角;钝角.25. 阅读理解:课外兴趣小组活动时,老师提出了如下问题:在中, , , 求边上的中线的取值范围. (1)、小明在组内经过合作交流,得到了如下的解决方法如图:
(1)、小明在组内经过合作交流,得到了如下的解决方法如图:
延长到使得;
再连接 , 把、、集中在中;利用三角形的三边关系可得 , 则的取值范围是▲ .(2)、感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
请写出图中与的位置关系并证明;(3)、思考:已知,如图 , 是的中线, , , , 试探究线段与的数量和位置关系,并加以证明.