山东省聊城市阳谷县重点中学2023-2024学年八年级上学期数学月考考试试卷（9月）

试卷更新日期：2023-11-06 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 点 $P (3 ， 4)$ 关于 $y$ 轴对称的点的坐标是（）

A、 $(3 ， - 4)$ B、 $(- 3 ， 4)$ C、 $(- 4 ， - 3)$ D、 $(- 4 ， 3)$

查看试题解析
3. 如图，为测量桃李湖两端AB的距离，南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C，测得∠ACB的度数，在AC的另一侧测得∠ACD=∠ACB，CD=CB，再测得AD的长，就是AB的长．那么判定△ABC≌△ADC的理由是（）

A、SAS B、SSS C、ASA D、AAS

查看试题解析
4. 用直尺和圆规作一个角等于已知角，如图，能得出 $∠ A O B = ∠ A' O' B'$ 的依据是（）

A、 $S A S$ B、 $A A S$ C、 $A S A$ D、 $S S S$

查看试题解析
5. 两个直角三角形全等的条件是（　　）

A、一个锐角对应相等 B、一条边对应相等 C、两条直角边对应相等 D、两个角对应相等

查看试题解析
6. 下列说法中：

①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；

②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；

③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．

正确的是（　　）

A、①和② B、②和③ C、①和③ D、①②③

查看试题解析
7. 观察下列尺规作图的痕迹：

其中，能够说明 $A B > A C$ 的是（）

A、①② B、②③ C、①③ D、③④

查看试题解析
8. 如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）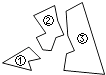

A、带①去 B、带②去 C、带③去 D、带①和②去

查看试题解析
9. 如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则△ACE的周长为（）

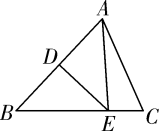A、8 B、11 C、16 D、17

查看试题解析
10. 近年来，高速铁路的规划与建设成为各地政府争取的重要项目，如图，A，B，C三地都想将高铁站的修建项目落户在当地．但是，国资委为了使A，B，C三地的民众都能享受高铁带来的便利，决定将高铁站修建在到A，B，C三地距离都相等的地方，则高铁站应建在（）

A、AB，BC两边垂直平分线的交点处 B、AB，BC两边高线的交点处 C、AB，BC两边中线的交点处 D、∠B，∠C两内角的平分线的交点处

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $△ A B C$ 的角平分线，若 $C D = 4$ ， $A C = 12$ ， $A B = 15$ ，则 $△ A B C$ 的面积为（）

A、 $24$ B、 $48$ C、 $54$ D、 $108$

查看试题解析
12. 如图，点 $B$ 、 $D$ 、 $E$ 、 $C$ 在同一直线上， $△ A B D$ ≌ $△ A C E$ ， $∠ A E C = 100 °$ ，则 $∠ D A E =$ （）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $80 °$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

13. 已知点 $A (m + 2 ， - 3)$ ， $B (- 2 ， n - 4)$ 关于 $x$ 轴对称，则 $m =$ ， $n =$ ．

查看试题解析
14. 如图，点A、B分别在x轴、y轴上， $O A = O B$ ，分别以点A、B为圆心，以大于 $\frac{1}{2} A B$ 长为半径画弧，两弧交于点P ．若点P的坐标为 $(a ， 3 a - 4)$ ，则a的值为．

查看试题解析
15. 如图所示，将矩形纸片 $A B C D$ 折叠，使点 $D$ 与点 $B$ 重合，点 $C$ 落在点 $C'$ 处，折痕为 $E F$ ，若 $∠ E F C' = 125 °$ ，那么 $∠ A B E$ 的度数为．

查看试题解析
16. 如图， $∠ M O N$ 内有一点 $P$ ， $P P_{1}$ 、 $P P_{2}$ 分别被 $O M$ 、 $O N$ 垂直平分， $P_{1} P_{2}$ 与 $O M$ 、 $O N$ 分别交于点 $A$ 、 $B .$ 若 $P_{1} P_{2} = 10 c m$ ，则 $△ P A B$ 的周长为 $c m$ ．

查看试题解析
17. 如图，在网格中与 $△$ ABC成轴对称的格点三角形一共有个．

查看试题解析

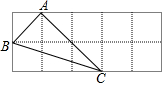
三、解答题（本大题共7小题，共69.0分。解答应写出文字说明，证明过程或演算步骤）

18. nbsp；如图， $A B = A E$ ， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D .$ 求证： $A C = A D$ ．

查看试题解析
19. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (- 4 ， 1)$ ， $B (- 3 ， 3)$ ， $C (- 1 ， 2)$ ．
⑴作出 $△ A B C$ 关于 $y$ 轴对称的 $△ A' B' C'$ ，并写出 $C'$ 的坐标．
⑵在 $x$ 轴上画出点 $P$ ，使 $P A + P C$ 最小，并写出点 $P$ 的坐标． $($ 不写作法，保留作图痕迹 $)$

查看试题解析
20. 如图，折叠直角三角形纸片，使直角顶点 $C$ 落在斜边上的点 $E$ 处，折痕为 $A D$ ， $∠ A D C = 70 °$ ，求 $∠ B$ 的度数．

查看试题解析
21. 作图题：在两条公路的交叉处有两个村庄 $C$ 、 $D$ 政府想在交叉处的内部建一个加油站 $P$ ，并且使加油站到村庄 $C$ 、 $D$ 的距离相等且到两条公路的距离也相等 $. ($ 保留作图痕迹，不写作法 $)$

查看试题解析
22. 如图，△ABC中，DE为AB的垂直平分线，交AC于点D，交AB于点E，若△ABC的周长为20，AE为4，求△BCD的周长．

查看试题解析
23. 如图，点 $D$ 、 $B$ 分别在 $∠ A$ 的两边上， $C$ 是 $∠ D A B$ 内一点， $A B = A D$ ， $B C = C D$ ， $C E ⊥ A D$ 于 $E$ ， $C F ⊥ A F$ 于 $F$ ，
求证： $C E = C F$ ．

查看试题解析
24. 如图，已知 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 ° .$ 分别过 $A$ 、 $B$ 向过点 $C$ 的直线作垂线，垂足分别为点 $M$ 、 $N$ ．

(1)、如图 $1$ ，过 $C$ 的直线与斜边 $A B$ 不相交时，求证： $M N = A M + B N$ ．

(2)、如图 $2$ ，过 $C$ 的直线与斜边 $A B$ 相交时，其他条件不变，若 $A M = 10$ ， $B N = 3$ ，试求 $M N$ 的长．

查看试题解析