山东省聊城市十八校联考2023-2024学年八年级上学期月考数学试卷(10月)
试卷更新日期:2023-11-06 类型:月考试卷
一、选择题(共12小题,每小题3分,在每小题给出的四个选项中,只有一项符合题目要求)
-
1. 下列图形是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON , 移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC , 由此作法便可得△NOC≌△MOC , 其依据是( )
2. 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON , 移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC , 由此作法便可得△NOC≌△MOC , 其依据是( ) A、SSS B、SAS C、ASA D、AAS3. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A、SSS B、SAS C、ASA D、AAS3. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )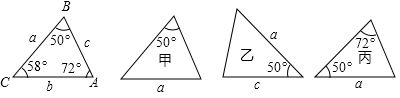 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙4. 如图,用尺规作出∠OBF=∠AOB , 所作痕迹( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙4. 如图,用尺规作出∠OBF=∠AOB , 所作痕迹( ) A、以点B为圆心,以CD长为半径的弧 B、以点D为圆心,以DC长为半径的弧 C、以点E为圆心,以BE长为半径的弧 D、以点E为圆心,以CD长为半径的弧5. 如图,已知 , 则下列条件中,不能使≌成立的是( )
A、以点B为圆心,以CD长为半径的弧 B、以点D为圆心,以DC长为半径的弧 C、以点E为圆心,以BE长为半径的弧 D、以点E为圆心,以CD长为半径的弧5. 如图,已知 , 则下列条件中,不能使≌成立的是( ) A、 B、 C、 D、6. 如图中△ABC≌△ADE , ∠DAC=100°,∠BAE=140°,则∠CFE的度数是( )
A、 B、 C、 D、6. 如图中△ABC≌△ADE , ∠DAC=100°,∠BAE=140°,则∠CFE的度数是( ) A、15° B、20° C、25° D、30°7. 如图所示,已知AB=AC , AE=AF , AE⊥EC于E , AF⊥BF于F , 则图中全等的三角形共有( )
A、15° B、20° C、25° D、30°7. 如图所示,已知AB=AC , AE=AF , AE⊥EC于E , AF⊥BF于F , 则图中全等的三角形共有( ) A、4对 B、3对 C、2对 D、1对8. 如图,在△ABC中,AB⊥AC , AB=3,BC=5,AC=4,EF垂直平分BC , 点P为直线EF上的任意一点,则△ABP周长的最小值是( )
A、4对 B、3对 C、2对 D、1对8. 如图,在△ABC中,AB⊥AC , AB=3,BC=5,AC=4,EF垂直平分BC , 点P为直线EF上的任意一点,则△ABP周长的最小值是( ) A、12 B、6 C、7 D、89. 如图,在 的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的 为格点三角形,在图中与 成轴对称的格点三角形可以画出( )
A、12 B、6 C、7 D、89. 如图,在 的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的 为格点三角形,在图中与 成轴对称的格点三角形可以画出( ) A、6个 B、5个 C、4个 D、3个10. 如图,△ABC≌△DEC , 点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD , 垂足为点F , 若∠BCE=65°,则∠CAF的度数为( )
A、6个 B、5个 C、4个 D、3个10. 如图,△ABC≌△DEC , 点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD , 垂足为点F , 若∠BCE=65°,则∠CAF的度数为( ) A、30° B、25° C、35° D、65°11. 如图,点E , F分别为长方形纸片ABCD的边AB , CD上的点,将长方形纸片沿EF翻折,点C , B分别落在点C',B'处.若∠DFC'=α,则∠FEA-∠AEB'的度数为( )
A、30° B、25° C、35° D、65°11. 如图,点E , F分别为长方形纸片ABCD的边AB , CD上的点,将长方形纸片沿EF翻折,点C , B分别落在点C',B'处.若∠DFC'=α,则∠FEA-∠AEB'的度数为( ) A、 B、 C、 D、12. 如图,在中, , , , 点为的中点,如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.若在某一时刻能使与全等.则点的运动速度为( )
A、 B、 C、 D、12. 如图,在中, , , , 点为的中点,如果点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.若在某一时刻能使与全等.则点的运动速度为( )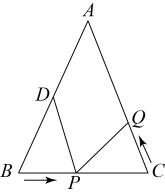 A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题(共5小题,共15分)
-
13. 为了落实“扶贫安居工程”,打造特色民居,工人师傅砌门时,常用木条EF、MN固定门框ABCD(如图),使其不变形,这种做法的根据是 .
 14. 若点A(1+m , 1-n)与点B(3,-2)关于y轴对称,则(m+n)2023的值是 .15. 如图,∠MON内有一点P , PP1、PP2分别被OM、ON垂直平分,P1P2与OM、ON分别交于点A、B . 若P1P2=10cm , 则△PAB的周长为cm .
14. 若点A(1+m , 1-n)与点B(3,-2)关于y轴对称,则(m+n)2023的值是 .15. 如图,∠MON内有一点P , PP1、PP2分别被OM、ON垂直平分,P1P2与OM、ON分别交于点A、B . 若P1P2=10cm , 则△PAB的周长为cm . 16. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.
16. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.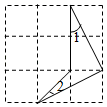 17. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),AB=5,∠OAB的平分线交x轴于点C , 点P、Q分别为线段AC、线段AO上的动点,则OP+PQ的最小值为 .
17. 如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),AB=5,∠OAB的平分线交x轴于点C , 点P、Q分别为线段AC、线段AO上的动点,则OP+PQ的最小值为 .
三、解答题(共8小题,共69分)
-
18. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , ,求 的大小.
 19. 已知:如图,点A、D、B、E在一条直线上,AC∥DF , BC∥EF , AC=DF , 求证:AD=BE .
19. 已知:如图,点A、D、B、E在一条直线上,AC∥DF , BC∥EF , AC=DF , 求证:AD=BE . 20. 如图,△ABC三个顶点的坐标分别为A(-4,1),B(-3,3),C(-1,2).
20. 如图,△ABC三个顶点的坐标分别为A(-4,1),B(-3,3),C(-1,2).
⑴作出△ABC关于y轴对称的△A′B′C′,并写出C′的坐标;
⑵求出△A′B′C′的面积;
⑶在x轴上画出点P , 使PA+PC最小,并写出点P的坐标.(不写作法,保留作图痕迹)
21. 将两个大小不同的含45°角的直角三角板按如图1所示放置,从中抽象出一个几何图形(如图2),B , C , E三点在同一条直线上,连接DC与AE交于点F .求证:DC⊥BE .
 22. 如图,在△ABC中,∠ACB=90°,AC=BC , BE⊥CE于E , AD⊥CD于D , DE=4cm , AD=6cm , 求CD的长.
22. 如图,在△ABC中,∠ACB=90°,AC=BC , BE⊥CE于E , AD⊥CD于D , DE=4cm , AD=6cm , 求CD的长. 23. 如图1,△ABC中,AB=9,AC=6,AD是中线,求AD得取值范围.(提示:延长AD到E , 使DE=AD , 连接BE , 证明△BED≌△CAD , 经过推理和计算使问题得到解决.)请回答:
23. 如图1,△ABC中,AB=9,AC=6,AD是中线,求AD得取值范围.(提示:延长AD到E , 使DE=AD , 连接BE , 证明△BED≌△CAD , 经过推理和计算使问题得到解决.)请回答: (1)、为什么△BED≌△CAD?写出推理过程;(2)、求出AD的取值范围;24. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E .
(1)、为什么△BED≌△CAD?写出推理过程;(2)、求出AD的取值范围;24. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E . (1)、若BC=10,求△ADE的周长.(2)、若∠BAC=115°,求∠DAE的度数.(3)、设直线DM、EN交于点O , 试判断点O是否在BC的垂直平分线上,并说明理由.25. 问题背景:
(1)、若BC=10,求△ADE的周长.(2)、若∠BAC=115°,求∠DAE的度数.(3)、设直线DM、EN交于点O , 试判断点O是否在BC的垂直平分线上,并说明理由.25. 问题背景: (1)、如图1:在四边形ABCD中,AB=AD , ∠BAD=120°,∠B=∠ADC=90°.E , F分别是BC , CD上的点.且∠EAF=60°.探究图中线段BE , EF , FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G . 使DG=BE . 连接AG , 先证明△ABE≌△ADG , 再证明△AEF≌△AGF , 可得出结论,他的结论应是 .
(1)、如图1:在四边形ABCD中,AB=AD , ∠BAD=120°,∠B=∠ADC=90°.E , F分别是BC , CD上的点.且∠EAF=60°.探究图中线段BE , EF , FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G . 使DG=BE . 连接AG , 先证明△ABE≌△ADG , 再证明△AEF≌△AGF , 可得出结论,他的结论应是 .探索延伸:
(2)、如图2,若在四边形ABCD中,AB=AD , ∠B+∠D=180°.E , F分别是BC , CD上的点,且∠EAF= ∠BAD , 上述结论是否仍然成立,并说明理由.