（人教版）2023-2024学年七年级数学上册 3.3 解一元一次方程（二）——去括号与去分母同步分层训练（基础卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 解方程1-2(2x-1)=x，以下去括号正确的是（）

A、1-4x-2=x B、1-4x+1=x C、1-4x+2=x D、1-4x+2=-x

查看试题解析
2. 解方程 $2 (x + 1) - 3 (x - 1) = 6$ 的步骤如图所示，则在每一步变形中，依据“等式的基本性质”有（）

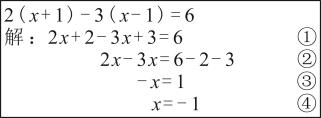A、①② B、②③ C、③④ D、②④

查看试题解析
3. 下列方程的变形中正确的是（）

A、由 $x + 5 = 6 x - 7$ 得 $x - 6 x = 7 - 5$ B、由 $- 2 (x - 1) = 3$ 得 $- 2 x - 2 = 3$ C、由 $\frac{x - 3}{0.7} = 1$ 得 $\frac{10 x - 30}{7} = 10$ D、由 $\frac{1}{2} x + 9 = - \frac{3}{2} x - 3$ 得 $2 x = - 12$

查看试题解析
4. 冉冉解方程 $- 3 (★ - 9) = 5 x - 1$ 时，发现★处一个常数被涂抹了，已知方程的解是 $x = 5$ ，则★处的数字是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 把方程 $\frac{x}{6} - \frac{x + 1}{3} = 2$ 去分母，下列变形正确的是（）

A、 $2 x - x + 1 = 2$ B、 $x - 2 (x + 1) = 12$ C、 $2 x - x + 1 = 12$ D、 $x - 2 (x + 1) = 2$

查看试题解析
6. 解方程 $2 x - (x + 10) = 5 x + 2 (x - 1)$ ，步骤如下：
去括号，得 $2 x - x - 10 = 5 x + 2 x - 2$     第一步
移项，得 $2 x - x - 5 x + 2 x = - 2 + 10$      第二步
合并同类项，得 $- 2 x = 8$                第三步
系数化为1，得 $x = - 4$                  第四步
以上解方程步骤中，开始出现错误的是（    ）

A、第一步 B、第二步 C、第三步 D、第四步

查看试题解析
7. 如果关于x的方程 $2 (x + a) - 4 = 0$ 的解是 $x = - 1$ ，那么a的值是（）．

A、3 B、-3 C、-1 D、1

查看试题解析
8. 在学习完“解方程”后，老师设计了一个接力游戏，规则是：每人只能看到前一人给出的结果，并进行一步计算再将结果传递给下一人，最后完成解方程，过程如图所示，接力中，自己负责的一步计算正确的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 方程 $2 - \frac{3 x - 7}{4} = - \frac{x + 17}{5}$ 去分母得（）.

A、2-5(3x-7)=-4(x+17) B、40-15x-35=-4x-68 C、40-5(3x-7)=-4x+68 D、40-5(3x-7)=-4(x+17)

查看试题解析
10. 方程 $(3 x + 2) - 2 (2 x - 1) = 0$ 去括号正确的是（）

A、 $3 x + 2 - 2 x + 1 = 0$ B、 $3 x + 2 - 4 x + 1 = 0$ C、 $3 x + 2 - 4 x - 2 = 0$ D、 $3 x + 2 - 4 x + 2 = 0$

查看试题解析

二、填空题

11. 若方程2x＝﹣6和方程3（x﹣a）＝7的解相同，则a＝.

查看试题解析
12. 解方程 $5 (x - 2) = 6 (\frac{x}{2} - \frac{1}{3})$ .有以下四个步骤，其中第①步的依据是.
解：①去括号，得 $5 x - 10 = 3 x - 2$ .

②移项，得 $5 x - 3 x = 10 - 2$ .

③合并同类项，得 $2 x = 8$ .

④系数化为1，得 $x = 4$ .

查看试题解析
13. 已知 $y_{1} = x + 2$ ， $y_{2} = 4 x - 7$ .当 $x =$ 时， $y_{1} - y_{2} = 0$

查看试题解析
14. 小明解方程 $\frac{2 x - 1}{3} = \frac{x + a}{2} - 3$ 去分母时，方程右边的﹣3忘记乘6，因而求出的解为x=2，则原方程正确的解为．

查看试题解析
15. 对于两个非零有理数a，b，规定：a⊗b＝ab－(a＋b)．若2⊗(x＋1)＝1，则x的值为．

查看试题解析

三、解答题

16. 用方程解答：x的3倍与1之和的二分之一等于x的四倍与1之差的三分之一，求x．

查看试题解析
17. 小李在解方程 $\frac{3 x + 5}{2} - \frac{2 x - m}{3} = 1$ 去分母时方程右边的1没有乘以6，因而得到方程的解为x=﹣4，求出m的值并符合题意解出方程．

查看试题解析
18. 下面是马小哈同学做的一道题，请按照“要求”帮他改正．
解方程： $\frac{3 x - 1}{2} = 1 + \frac{2 x + 3}{3}$

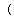马小哈的解答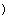

解： $3 (3 x - 1) = 1 + 2 (2 x + 3)$

$9 x - 3 = 1 + 4 x + 6$

$9 x - 4 x = 1 + 6 - 3$

$5 x = 4$

$x = \frac{4}{5}$

“要求”：

$①$ 用“-”画出解题过程中的所有不符合题意．

$②$ 请你把正确的解答过程写在下面．

查看试题解析
19. 依据下列解方程 $\frac{0.3 x + 0.5}{0.2} - 1 = \frac{2 x - 1}{3}$ 的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据．
解：原方程可变形为 $6 \times \frac{0.3 x + 0.5}{0.2} - 6 \times 1 = 6 \times \frac{2 x - 1}{3}$ （                          ）
去分母，得 $3 (3 x + 5) - 6 = 2 (2 x - 1)$ （                            ）
去括号，得 $9 x + 15 - 6 = 4 x - 2$ （                                ）
（          ），得 $9 x - 4 x = - 2 - 15 + 6$ （                              ）
合并同类项，得 $5 x = - 11$
系数化为1，得 $x = - \frac{11}{5}$ （                          ）

查看试题解析

四、综合题

20.

(1)、老师在黑板上出了一道解方程的题 $\frac{2 x - 1}{3} = 1 - \frac{x + 2}{4}$ ，小明马上举手，要求到黑板上做，他是这样做的：
$4 (2 x - 1) = 1 - 3 (x + 2)$ ……………… …①

$8 x - 4 = 1 - 3 x - 6$ …………………… …②

$8 x + 3 x = 1 - 6 + 4$ …………………… …③

$11 x = - 1$ ………………………………… ④

$x = - \frac{1}{11}$ ………………………………… ⑤

老师说：小明解一元一次方程的一般步骤都知道却没有掌握好，因此解题时有一步出现了不符合题意，请你指出他错在（填编号）；

(2)、然后，你自己细心地解下面的方程：
$\frac{2 x + 1}{6} + \frac{x - 1}{3} = 1$

(3)、 $\frac{2 y - 1}{4} - 1 = \frac{5 y - 7}{6}$

查看试题解析
21.

(1)、小玉在解方程 $\frac{2 x - 1}{3} = \frac{x + 8}{2} - 1$ 去分母时，方程右边的“﹣1”项没有乘6，因而求得的解是x=10，试求a的值．

(2)、当m为何值时，关于x的方程5m+3x=1+x的解比关于x的方程2x+m=5m的解大2？

查看试题解析
22. 已知关于 $x$ 的方程： $2 (x - 1) + 1 = x$ 与 $3 (x + m) = m - 1$ 有相同的解.

(1)、求 $m$ 的值

(2)、求以 $y$ 为未知数的方程 $\frac{3 - m y}{3} = \frac{m - 3 x}{2}$ 的解.

查看试题解析
23. 如果两个方程的解相差1，则称解较大的方程为另一个方程的“后移方程”.
例如：方程 $x - 2 = 0$ 是方程 $x - 1 = 0$ 的后移方程.

(1)、判断方程 $2 x + 1 = 0$ 是否为方程 $2 x + 3 = 0$ 的后移方程（填“是”或“否”）；

(2)、若关于x的方程 $3 x + m = 0$ 是关于x的方程 $2 (x - 2) = - 4 (3 + x)$ 的后移方程，求m的值.

查看试题解析

（人教版）2023-2024学年七年级数学上册 3.3 解一元一次方程（二）——去括号与去分母 同步分层训练（基础卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册 3.3 解一元一次方程（二）——去括号与去分母同步分层训练（基础卷）