（人教版）2023-2024学年七年级数学上册 3.2 解一元一次方程（一）——合并同类项与移项同步分层训练（提升卷）

试卷更新日期：2023-11-06 类型：同步测试

进入出卷网下载

一、选择题

1. 小明在解关于x的方程5a+x=10时，误将“+x”看作“-x”，得方程的解为x=3，则原方程的解为（）

A、x=-4 B、x=-3 C、x=-2 D、x=-1

查看试题解析
2. 解方程 $\frac{x + 1}{3} - \frac{x - 1}{6} = 1$ 需下列四步，其中开始发生错误的一步是（）

A、去分母，得2(x+1)-(x-1)= 6 B、去括号，得2x+2-x+1=6 C、移项，得2x-x=6-2+1 D、合并同类项，得x= 5

查看试题解析
3. 若式子-2a+1与a-2的值相等，则a等于（）

A、1 B、2 C、-1 D、-2

查看试题解析
4. 嘉琪在进行解方程的思维训练，其中有一个方程“2y- $\frac{1}{2}$ = $\frac{1}{2}$ y+■”中的■没印清晰，嘉琪问老师，老师只是说：“■是一个有理数，该方程的解与当×= 2时代数式5(x-1)-2(x- 2)-4的值相同．”嘉琪很快补上了这个有理数．你认为嘉琪补的这个有理数是（）

A、1 B、-1 C、2 D、-2

查看试题解析
5. 已知 $(k - 1) x^{∣ k ∣} + 3 = 0$ 是关于 $x$ 的一元一次方程．则此方程的解是（）

A、-1 B、 $- \frac{3}{2}$ C、 $\frac{3}{2}$ D、±1

查看试题解析
6. 若关于 $x$ 的方程 $k x - 2 x = 14$ 的解是正整数，则 $k$ 的整数值有个．（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知关于x的方程2x+a=1-x与方程2x-3=1的解相同，则a的值为（）

A、2 B、-2 C、5 D、-5

查看试题解析
8. 小亮在解方程 $3 a + x = 7$ 时，由于粗心，错把 $+ x$ 看成了 $- x$ ，结果解得 $x = 2$ ，则 $a$ 的值为（）

A、 $a = \frac{5}{3}$ B、 $a = 3$ C、 $a = - 3$ D、 $a = \frac{3}{5}$

查看试题解析
9. 解方程5x-3=2x+2，移项正确的是（）

A、5x-2x=3+2 B、5x+2x=3+2 C、5x-2x=2-3 D、5x+2x=2-3

查看试题解析
10. 方程 $x - 4 = - x$ 与方程 $5 x - 2 (x + k) = 2 x$ 的解相同，则代数式 $k^{2} - 1$ 的值为（）

A、 $1$ B、 $- 1$ C、 $0$ D、 $2$

查看试题解析

二、填空题

11. 若方程2x+a＝1与方程3x-1＝2x+2的解相同，则a的值为．

查看试题解析
12. 若3x^m+5y³与 $\frac{2}{3}$ x²yⁿ的差仍为单项式，则m+n＝．

查看试题解析
13. 如图是一个数表，现用一个矩形在数表中任意框出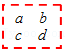4个数，当a+b+c+d＝32时，a＝．

查看试题解析
14. 已知m为非负整数，若关于x的方程mx=2-x的解为整数，则m的值为.

查看试题解析
15. 代数式2x＋5与x＋8的值相等，则x的值是.

查看试题解析

三、解答题

16. 已知关于x的方程 $2 (x - 1) = m + 4 + x$ 的解是-3的相反数，求m的值．

查看试题解析
17. 已知2x-12与x+3互为相反数，求x的值.

查看试题解析
18. 若方程 $2 x - 3 = 11$ 与关于 $x$ 的方程 $4 x + 5 = 3 k$ 有相同的解，求 $k$ 的值.

查看试题解析
19. 已知关于x的方程 $a x + 14 = 2 x + a$ 的解是3，求式子 $a^{2} + 2 (a - 3)$ 的值.

查看试题解析

四、综合题

20. 如图所示，数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位长度到达点C点.

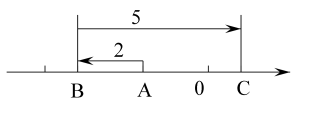(1)、求动点A所走过的路程及A、C之间的距离.

(2)、若C表示的数为1，则点A表示的数为.

查看试题解析
21. 已知“□－7＝△＋3”，其中□和△分别表示一个实数．

(1)、若□表示的数是3，求△表示的数；

(2)、若□和△表示的数互为相反数，求□和△分别表示的数；

查看试题解析
22. 定义：若关于x的一元一次方程ax＝b的解为b+a，则称该方程为“和解方程”，例如：2x＝﹣4的解为x＝﹣2，且﹣2＝﹣4+2，则该方程2x＝﹣4是和解方程.

(1)、判断﹣3x＝ $\frac{9}{4}$ 是否是和解方程，说明理由；

(2)、若关于x的一元一次方程 -x＝m﹣2是和解方程，求m的值.

查看试题解析
23. 历史上的数学巨人欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ 来表示，即 $f (x) = x^{2} + 3 x - 5$ ，例如：当 $x = 1$ 时，多项式 $x^{2} + 3 x - 5$ 的值记为 $f (1) = 1^{2} + 3 \times 1 - 5$ =1。

(1)、已知 $f (x) = - 2 x^{2} - 3 x + 1$ ，分别求出 $f (- 1)$ 和 $f (- 2)$ 的值。

(2)、已知 $f (x) = a x^{3} + 2 x^{2} - x - 14$ ， $f (\frac{1}{2}) = a$ ，求 $a$ 的值。

查看试题解析

（人教版）2023-2024学年七年级数学上册 3.2 解一元一次方程（一）——合并同类项与移项 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册 3.2 解一元一次方程（一）——合并同类项与移项同步分层训练（提升卷）